Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 10.1 - Ex. 52

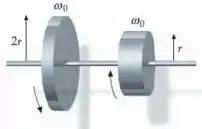
Dois discos de massa idêntica mas raios diferentes ( r e 2 r ) estão girando em torno de um eixo sem atrito, com a mesma rapidez angular ω 0 , mas em sentidos opostos. Os dois discos são lentamente aproximados. A força de atrito entre as superfícies faz com que eles passem a ter a mesma velocidade angular final. (a) Qual é a magnitude da velocidade angular final, em termos de ω o ? (b) Qual é a variação da energia cinética de rotação do sistema? Explique.

Passo 1

Obs: Antes de começar, corrigimos no enunciado o símbolo da rapidez angular. Ele dá como θ 0 , mas esse é o símbolo da posição angular inicial. O símbolo da rapidez angular inicial deve ser ω 0 . Vamos usar esse ultimo símbolo, ok?

a) Vamos avaliar nossa situação. Temos discos separados que se juntam. Repara que em nenhum momento ele fala que houve uma força externa causando um torque externo, ou mesmo um torque externo aplicado, logo podemos usar a conservação de momento angular.

O atrito entre os discos não vai ser uma força externa, e sim interna ao sistema (entre os discos).

Inicialmente temos dois discos (cada um com seu momento de inércia) girando com rapidez angular de mesmo módulo ω 0 , mas em sentidos opostos. Mais tarde os dois estarão juntos girando com uma única rapidez angular ω f . Logo a conservação de momento fica

L o = L f

I 1 ω 0 + I 2 - ω 0 = I 1 + I 2 ω f

I 1 ω 0 - I 2 ω 0 = I 1 + I 2 ω f

E então:

ω f = I 1 - I 2 I 1 + I 2 ω 0

Passo 2

E a fórmula geral para o momento de inércia de um disco de massa M e raio R é:

I = 1 2 M R 2

De forma que:

I 1 = 1 2 m 2 r 2 = 2 m r 2

I 2 = 1 2 m r 2

Vamos substituir isso na expressão anterior para encontrar a magnitude da velocidade angular final:

ω f = 2 m r 2 - 1 2 m r 2 2 m r 2 + 1 2 m r 2 ω 0

Dividindo o numerador e o denominador por m r 2 :

ω f = 2 - 1 2 2 + 1 2 ω 0 = 3 5 ω 0

Passo 3

(b) Vamos lembrar da fórmula para a energia cinética de rotação:

K r o t = 1 2 I ω 2

E então a variação de energia cinética é:

Δ K r o t = K r o t f - K r o t i

Δ K r o t = 1 2 I 1 + I 2 ω f 2 - 1 2 I 1 ω 0 2 + 1 2 I 2 ω 0 2

Agora é só substituir com as expressões que já encontramos:

Δ K r o t = 1 2 I 1 + I 2 3 5 ω 0 2 - 1 2 I 1 + I 2 ω 0 2

Δ K r o t = 1 2 I 1 + I 2 ω o 2 9 25 - 1

Δ K r o t = - 16 25 1 2 I 1 + I 2 ω 0 2

E a expressão entre parênteses é simplesmente a energia cinética inicial do sistema:

Δ K r o t = - 16 25 K o

E podemos explicar essa perda de energia em termos do atrito entre os dois discos.

Resposta

(a) ω f = 3 5 ω 0 .

(b) Δ K r o t = - 16 25 K 0 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ordene em sequência decrescente os módulos das acelerações angulares de α a a α d na FIGURA Q12.11. Explique o seu ordenamento.
A FIGURA P12.82 mostra duas bolas de argila aproximando-se uma da outra.a. Calcule o momentum angular total em relação à origem neste instante.b. Calcule o momentum angular total um instante antes da
Seguindo em direção ao cume do Pico Pike, um avião de massa 12000k g voa sobre as planícies do Kansas a uma altitude praticamente constante de 4,30k m com velocidade constante de 1 75m / s a oeste. Qu
Uma partícula de massa 0,400k g é presa à marca de 100c m de uma régua de massa 0,100k g . A régua gira sobre a superfície de uma mesa horizontal sem atrito com velocidade angular de 4,00r a d / s . C
O vetor posição de uma partícula de massa de 2,00k g como função de tempo é dado por r →=( 6,00 i ^+5,00 t j ^ ) , onde r → está em m e t r o s e t em s e g u n d o s . Determine o momento angular da