Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 20.Exercícios e Problemas - Ex. 6

A Figura 20.12 mostra um capacitor cilíndrico preenchido por um material dielétrico de resistividade elétrica ρ e constante dielétrica κ . Uma bateria aplica uma voltagem V ao capacitor.

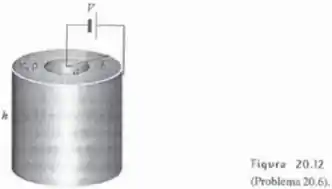
a) Calcule a corrente I e a resistência R entre as placas.

b) Mostre que a constante de tempo R C do capacitor tem o mesmo valor ρ κ ϵ 0 obtido para o capacitor de placas paralelas no 20.5P.

Passo 1

Vamos começar calculando a resistência entre as placas. Para isso, vamos compor o cilindro por várias cascas cilíndricas infinitesimais de raio r e espessura d r . A resistência infinitesimal dessa casquinha cilíndrica será

d R = ρ A c a s c a d r

Note que o d r faz o papel do comprimento. A área da casca cilíndrica é simplesmente a área lateral do cilindro de raio r e altura h :

A c a s c a = 2 π r h

Portanto,

d R = ρ 2 π h d r r

Para achar a resistência, basta integrar de r = a até r = b :

R = ρ 2 π h ∫ a b d r r → R = ρ 2 π h ln ⁡ b a

Para achar a corrente, basta lembrar que

V = R I

Assim,

I = V R → I = 2 π h V ρ ln ⁡ b a

Passo 2

No capítulo 17 vimos que a capacitância do capacitor de placas paralelas no vácuo era

C v a c u o = 2 π ϵ 0 h ln ⁡ b a

No meio com permissividade elétrica ϵ , a capacitância é

C = 2 π ϵ h ln ⁡ b a

Lembrando que ϵ = κ ϵ 0 , temos que

C = 2 π κ ϵ 0 h ln ⁡ b a

Passo 3

Multiplicando a resistência pela capacitância:

R C = ρ 2 π h ln ⁡ b a ⋅ 2 π κ ϵ 0 h ln ⁡ b a

Simplificando o que der para simplificar, achamos

R C = ρ κ ϵ 0

Resposta

R = ρ 2 π h ln ⁡ b a

I = 2 π h V ρ ln ⁡ b a

R C = ρ κ ϵ 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um fio de extensão consiste em um par de fios de cobre 16 de 30 m de comprimento. Qual é a diferença de potencial que deve ser aplicada a um dos fios se ele deve conduzir uma corrente de 5,0A ?
Um fio de 10m de comprimento tem uma resistência igual a 0,20Ω e conduz uma corrente igual a 5,0A . (a) Qual é a diferença de potencial no comprimento total do fio?(b) Qual é a intensidade do campo el
Qual é o comprimento de um fio de cobre calibre 14 que tem resistência de 12,0Ω ? (b) Que corrente ele conduzirá se uma diferença de potencial de 120V for aplicada em todo seu comprimento?
Um cilindro de vidro de 1,00c m de comprimento tem resistividade de 1,01 × 10 12Ω ⋅ m . Que comprimento de fio de cobre com a mesma área transversal terá a mesma resistência que o cilindro de vidro?
Um bloco de carbono tem 3,0c m de comprimento e seção transversal quadrada cujos lados têm 0,50c m de comprimento. Uma diferença de potencial de 8,4V é mantida no seu comprimento. (a) Qual é a resistê