Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 19.Exercícios e Problemas - Ex. 12
Considere bolas de sinuca de raio , dispersadas de forma aleatória sobre a mesa, com densidade (bolas por unidade de área) . Mostre que o livre percurso médio de uma bola adicional posta a rola sobre a mesa é .
Passo 1
O livre percurso médio é a distância média percorrida pela bola de sinuca antes de se chocar com outra bola parada na mesa.
Para resolver esse problema, vamos considerar uma seção de choque de tamanho e uma distância percorrida pela bola entre duas colisões sucessivas:
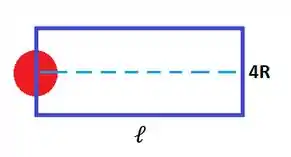
A área da região “varrida” bela bola é
Passo 2
Para que seja o livre percurso médio, nessa região deve existir em média apenas uma bola da mesa. Com isso, montamos a regrinha de três:
Observe que em uma unidade de área temos bolas, e na área temos uma bola. Multiplicando em cruz:
Daí,
Observe que quanto maior o tamanho das bolinhas () ou quanto maior a densidade de bolinhas na mesa (), menor será o livre caminho médio, o que faz bastante sentido 😉!
Resposta
Demonstração.