Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 29.2 - Ex. 14
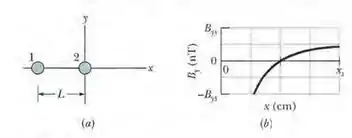
Na figura 29-45a mostra, em seção reta, dois fio longos e paralelos, percorridos por correntes e separados por uma distância . A razão entre as correntes é ; os sentidos das correntes não são conhecidos. A figura 29-45b mostra a componente do campo magnético em função da posição no eixo à direita do fio 2. A escala vertical é definida por e a escala horizontal por . (a) Para que valor de a componente é máxima? (b) Se , qual é o valor máximo de ? Determine o sentido (para dentro ou para fora do papel) (c) de (d) de .
Passo 1
Fala aí! tudo certinho? 😁
Nesse problema temos dois fio longos e paralelos, percorridos por correntes e separados por uma distância . Os sentidos das correntes não são conhecidos e . A figura mostra a componente do campo magnético em função da posição no eixo à direita do fio 2. A escala vertical é definida por e a escala horizontal por . a patir daí queremos obter para que valor de a componente é máxima. Se , qual é o valor máximo de ? E também determine o sentido (para dentro ou para fora do papel) de de .
Tem ideia de como fazer isso? 🤔
Passo 2
O fato de que para no gráfico da figura 29-49b siginifica que as correntes têm sentidos opostos. Assim, de acordo com a equação para fios longos:
Para maximizar , derivamos a expressão anterior em relação a e igualamos o resultado a zero, o que nos dá:
A única raiz positiva da equação anterior é , para qual . Para determinar o valor de , fazemos na expressão de e igualamos o resultado a zero, o que nos dá:
A componente é máxima para .
Para , temos:
E aí! entendeu tudo? Responde Aí! 😎
Resposta
a) A componente é máxima para ;
b) ;
c) e d) a figura 29-49b mostra que em pontos muito próximos do fio 2, nos quais a contribuição do fio 2 é muito maior que a do fio 1, aponta no sentido negativo do eixo . De acordo com a regra da mão direita, isso indica que o sentido da corrente no fio 2 é para dentro fo papel. Como sabemos que as correntes têm sentidos opostos, isso indica também que o sentido da corrente no fio 1 é para fora do papel.