Na figura 29-61, e . Determine (a) o módulo e (b) o sentido (para dentro ou para fora do papel) do campo magnético no ponto .
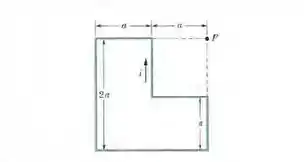
Passo 1
E aí, pessoal! 😎
Nesse problema temos um fio percorrido por uma corrente e nosso objetivo é obter o modulo e sentido do campo magnético no ponto .
Parece complicado? 😉
O campo magnético em é a soma vetorial dos campos produzidos por cada trecho retilíneo do fio. Então vamos ter que calcular a contribuição de cada trecho separadamente e somar tudo.
Vamos iniciar olhando as partes retilíneas colineares a . A lei de Biot-Savart nos diz que para os dois elementos retilíneos, o ângulo entre é zero e . Por conta disso, o produto vetorial vai ser zero e o campo nulo:
Resumindo, trechos colineares não vão contribuir.
Já pros outros trechos, temos uma formulinha perfeita que descreve o campo gerado por um FIO RETILÍNEO finito:
Em que:
- é a distância perpendicular do ponto ao fio;
- e são os ângulos entre a direção do fio e as retas que ligam até as extremidades do fio;
- é a permeabilidade magnética do vácuo.
Então é isso, vamos avaliar cada trecho e somar tudo.
Veja só! 😊
Passo 2
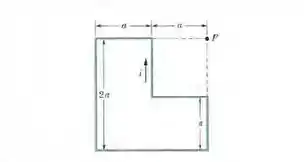
Vamos olhar primeiro pro trecho vertical maior, de tamanho . Pra esse trecho, temos:
Portanto, o campo será:
E pela regra da mão direita, essa contribuição vai ser saindo da página.
Agora, apenas ppor similaridade, eu vou escolher o outro trecho de tamanho , o pedaço horizontal mais de baixo. Ele tem todos os mesmos valores de , dos ângulos e o sentido do campo também é saindo da página.
Então pro trecho horizontal de tamanho , também temos:
Passo 3
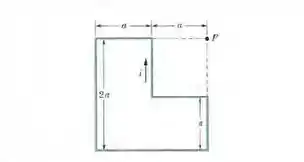
Agora vamos pegar aquele trechinho vertical ali do meio, o que não é colinear com .
Pra esse trecho, temos:
Mas antes de calcular, vamos perceber que o sentido vai ser entrando na página (regra da mão direita), porque aí a gente já acerta o sinal!
Portanto, o campo será:
E bem, pro trecho horizontal do meio, também vai ser igual (esse sistema carrega muitas simetrias). Mesmos ângulos, mesma distância, então mesmo campo magnético:
Passo 4
Agora vamos somar tudo:
Sendo esse sinal de menos aí significando que o campo está entrando na página (conforme usamos nos passos 2 e 3). Mas vamos fazer isso em módulo agora, vai, não se confunde não!
O sentido do campo é para dentro do papel.
Sacou tudo? Responde Aí! 😁
Resposta
- O sentido do campo é para dentro do papel.