Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.4 - Ex. 12
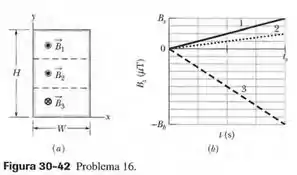
A figura 30-42a mostra um fio que forma um retângulo ( e tem uma resistência de Ω. O interior do retângulo é dividido em três partes iguais, que são submetidas a campos magnéticos , e . Os campos são uniformes dentro de cada região e orientados para fora do papel. A figura 30-42b mostra a variação das componentes dos três campos com o tempo ; a escala do eixo vertical é definida por e e a escala do eixo horizontal é definida por . Determine (a) o módulo e (b) o sentido da corrente induzida no fio.
Passo 1
Bom, galera, o módulo da força eletromotriz induzida em uam espira condutora é igual à taxa de variação com o tempo do fluxo magnético que atravessa a espira. A expressão para caluclar a força eletromotriz é a seguinte:
O sinal negativo mostra que a força eletromotriz se opõe à variação do fluxo.
Inicialmente, é interessante definir uma referência de positivo e negativo para os campos. Vamos dizer que os campos que estão saindo da folha sejam positivos e os que estão entrando são negativos. Assim, e são positivos e é negativo. Desse modo, a força eletromotriz induzida é:
Assim, de acordo com a lei de Ohm, valor absoluto da corrente é:
Passo 2
Assim, de acordo com a lei de Lenz, o sentido da corrente induzida é o sentido anti-horário.
Resposta
- ;
- O sentido, de acordo com a lei de Lenz, da corrente induzida é o sentido anti-horário.