Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 32.2 - Ex. 2
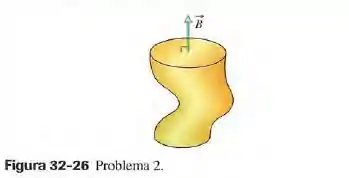
A figura 32-36 mostra uma superfície fechada. Na face plana superior, que tem um raio de , um campo magnético perpendicular de módulo aponta para fora. Na face plana inferior, um fluxo magnético de é dirigido para fora. Determine (a) o módulo e (b) o sentido (para dentro ou para fora) do fluxo magnético através da parte lateral da superfície.
Passo 1
Sabemos que o fluxo magnético através de uma superfície é dado por:
O fluxo através da face superior é , na qual . De acordo com o enunciado, o fluxo através da face inferior é . De acordo com a lei de Gauss, o fluxo total que passa por uma gaussiana é zero. Se o fluxo total é zero, o fluxo através das faces laterais deve ser negativo e igual, em valor absoluto, à soma dos fluxos através das faces superior e inferior. Assim,
Passo 2
O fato de que o fluxo através das faces laterais é negativo significa que o sentido do fluxo é para dentro.
Resposta
- ;
- O fato de que o fluxo através das faces laterais é negativo significa que o sentido do fluxo é para dentro.