Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 30.5 - Ex. 33
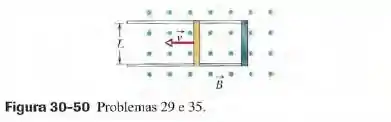
A barra condutora da figura 30-50 tem comprimento e está sendo puxada sobre os trilhos horizontais condutores, sem atrito, com velocidade constante . Os trilhos estão ligados em uma das extremidades por uma fita condutora. Um campo magnético uniforme , orientado para fora do papel, ocupa a região na qual se move a barra. Suponha que . Determine (a) o módulo e (b) o sentido (para cima ou para baixo) da força eletromotriz induzida na barra. Determine também (c) o valor absoluto e (d) o sentido da corrente na espira formada pela barra, os trilhos e a fita. Suponha que a resistência da barra é e que a resistência dos trilhos e da fita é desprezível. (e) Qual é a taxa com a qual a energia é dissipada na barra em forma de calor? (f) Qual é o módulo da força externa que deve ser aplicada à barra para que continue a se mover com velocidade ? (g) Qual é a taxa com a qual a força realiza trabalho sobre a barra?
Passo 1
Quando temos uma espira se movendo sob a influência de um campo magnético, a força eletromotriz assume uma cara diferente da que conhecemos. Seja o campo magnético, a largura da espira e o comprimento da espira que está na região com campo magnético. Da lei de Faraday, sabemos que:
O fluxo magnético, nessa situação, é dado por:
Aplicando na lei de Faraday, temos:
Assim, na nossa questão queremos saber a força eletromotriz induzida na barra. Vamos aplicar a expressão acima:
Passo 2
De acordo com a lei de Lenz, o sentido da força eletromotriz induzida é no sentido horário. Isso significa que, na barra, o sentido da fem é para cima.
Passo 3
De acordo com a primeira lei de Ohm,
Nesse caso, o sentido da corrente é o sentido horário.
Passo 4
A potência dissipada na barra é dada por:
Passo 5
A força que o campo magnético exerce sobre a barra é dada por . Fazendo uso da regra da mão direita, descobrimos que a força que o capo magnético exerce sobre a barra aponta para a direita e tem módulo
Para manter a barra em movimento com velocidade constante, é preciso aplicar uma força de mesmo módulo no sentido da direita para a esquerda. A resposta é, portanto,
Passo 6
A taxa com a qual a força externa realiza trabalho sobre a barra é:
Como toda a energia fornecida pela força externa é convertida em energia térmica, este valor é igual ao da taxa com a qual energia é dissipada na barra em forma de calor, calculado no item e.
Resposta
- ;
- O sentido da fem é para cima;
- ;
- O sentido da corrente é o sentido horário;
- ;
- ;
- .