Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 33.6 - Ex. 61
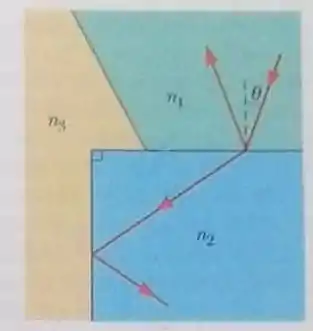
Na figura 33-59, um feixe luminoso que estava se propagando no meio 1 é refratado para o meio 2, atravessa esse meio e incide com o ângulo Crítico na interface dos meios 2 e 3. Os índices de refração são , e . (a) Qual é o valor do ângulo ? (b) Se o valor de aumentar, a luz conseguirá penetrar o meio 3?
Passo 1
Para resolver essa questão utilizaremos a Lei de Snell
Além da Relação fundamental da trigonometria, que diz
Passo 2
a) Na situação apresentada, nota-se que o complemento do ângulo de difração do meio 2 é o ângulo crítico mencionado. Dessa maneira, podemos fazer:
Usando a relação fundamental da trigonometria, temos
Dessa forma, podemos escrever:
Consequentemente o ângulo procurado é, substituindo os valores dados:
Passo 3
b) Sim. Conforme aumenta, o ângulo de incidência da luz na interface entre os meios 2 e 3 diminui, ficando menor que ângulo crítico. Dessa forma temos que parte da luz é transmitida para o meio 3.
Resposta
a) O ângulo procurado é .
b) Sim.