Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 33.6 - Ex. 63

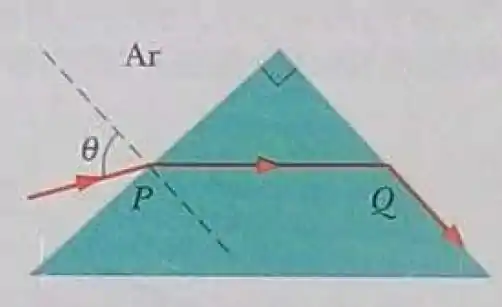
Na figura 33-60, um raio luminoso penetra no ponto P, com um ângulo de incidência θ , em um prisma triangular cujo ângulo do vértice superior é 90 graus. Parte da luz é refratada no ponto Q com um ângulo de refração de 90 graus. (a) Qual é o índice de refração do prisma em termos de θ ? (b) Qual, numericamente, é o maior valor possível do índice de refração do prisma? (c) A luz sairá do prisma no ponto Q se o ângulo de incidência nesse ponto for ligeiramente aumentado? (d) A luz sairá do prisma no ponto Q se o ângulo de incidência nesse ponto for ligeiramente reduzido?

Passo 1

(a)

Seja θ 1 o ângulo de incidência, seja θ 2 o ângulo de refração na primeira superfície e seja θ 3 o ângulo de incidência na segunda superfície. O ângulo de refração na segunda superfície é θ 4 = 90 . As normais à primeira e à segunda superfícies são mutuamente perpendiculares. Como a soma dos ângulos internos do triângulo formado pelo raio luminoso e as duas normais é 180, logo θ 3 = 90 - θ 2 e

s e n θ 3 = s e n 90 - θ 2 = c o s θ 2 = 1 - s e n 2 θ 2

Na segunda superfície, pela Lei de Snell temos que

n s e n θ 3 = s e n θ 4 = 1 ⇒ n 1 - s e n 2 θ 2 = 1

Já na segunda superfície, por uma análise parecida temos que

n 1 - s e n 2 θ 1 n 2 = 1 ⇒ n = 1 + s e n 2 θ 1

Passo 2

b) A função trigonometrica s e n 2 θ possui valor máximo 1. Dessa forma, o maior valor possível de n é

n m a x = 1 + 1 = 2  

Passo 3

c) Sim. Se o ângulo de incidência na primeira superfície for maior que θ 1 , o ângulo de refração será maior que θ 2 e o ângulo de incidência na segunda superfície será menor que θ 3 = 90 - θ 2 .Dessa forma, o ângulo de incidência na segunda superfície será menor que ângulo crítico para reflexão interna total e a luz sairá do prisma.

Passo 4

d) Não. Se o ângulo de incidência na primeira superfície for menor que θ 1 , o ângulo de refração será menor que que θ 2 e o ângulo de incidência na segunda superfície será maior que que θ 3 . Assim, o ângulo de incidência na segunda superfície será maior que o ângulo crítico para reflexão interna total e toda a luz será refletida para o interior do prisma.

Resposta

a) O índice de refração em termos do ângulo é n = 1 + s e n 2 θ 1

b) O valor máximo no índice de refração é n = 2 .

c) Sim.

d) Não.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na figura 33-62, um raio luminoso incide com um ângulo θ em uma face de um cubo de plástico transparente feito de um material cijo índice de refração é 1,56. As dimensões indicadas na figura são H = 2
Um raio de luz branca que estava se propagando no quartzo fundido incide em uma interfacequartzo-ar com um ângulo θ 1 . Suponha que o índice de refração do quartzo é n = 1,456 na extremindade vermelha
O ângulo crítico para a reflexão interna total em uma interface que separa um líquido do ar é 42,5 ° . a) Sabendo que um raio de luz proveniente do líquido incide sobre a interface com um ângulo de in
No final da série de óperas de Wagner, O Anel dos Nibelungos. Brunhilda tira o anel de ouro do dedo de Siegfried e joga-o dentro do Reno, onde o anel submerge até o fundo. Supondo que anel fosse peque
Um feixe de luz está se propagando dentro de um cubo sólido de vidro com índice de refração 1,53 . O feixe atinge a superficie do cubo a partir de dentro. a) Se o cubo está no ar, com que ângulo mínim