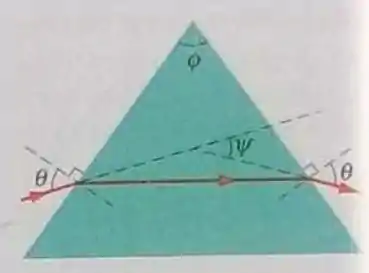
Suponha que o ângulo do vértice superior do prisma de vidro da fig 33-53 seja e que o índice de refração do vidro seja . (a) Qual é o menor ângulo de incidência para o qual um raio pode entrar na face esquerda do prisma e sair na face direita? (b) Qual deve ser o ângulo de incidência para que o raio saia do prisma com o mesmo ângulo com que entrou, como na fig 33-53?

(a) Seja A o ponto de entrada no prisma do raio luminoso (o ponto onde o raio encontra a superfície esquerda do prisma), de B o vértice superior do prisma e de C o ponto de saída do raio. Vamos chamar de o ângulo entre a reta AB e a direção do raio no interior do prisma (o complemento do ângulo de refração na primeira superfície) e de o ângulo entre a reta BC e a direção do raio no interior do prisma ( o complemento do ângulo de incidência na segunda superfície). Quando o ângulo do raio incidente tem o menor valor necessário para que a luz saia do prisma, o ângulo de incidência na segunda superfície é o ângulo crítico para reflexão interna total e o ângulo de refração na segunda superfície é 90 graus. Seja o ângulo de incidência na segunda superfície. Pela Lei de Snell temos:

Devido à soma dos ângulos internos de um triângulo é 180 graus, temos que

Assim .

Aplicando a Lei de Snell na primeira superfície, temos:”