Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 33.Problemas Adicionais - Ex. 75

Na figura 33-65, um raio luminoso entra em uma placa de vidro no ponto A, com um ângulo de incidência θ 1 = 45,0 ° , e sofre reflexão interna total no ponto B. De acordo com essas informações, qual é o valor mínimo do índice de refração do vidor?

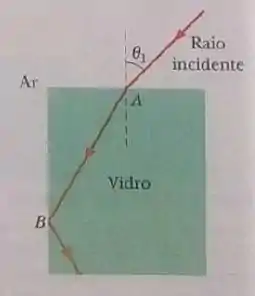
Passo 1

Do enunciado temos que θ 1 = 45,0 ° e que o reio luminoso sofre reflexão interna total no ponto B.

Vamos supor que θ 2 seja o ângulo de refração na primeira superfície e θ 3 seja o ângulo de incidência na segunda superfície. A condição para que haja reflexão interna total na segunda superfície é n   s e n   θ 3 ≥ 1 .

O raio luminoso está passando do ar para o vidro. Sabemos que o índice de refração do ar é aproximadamente 1, deta forma aplicando a lei de Snell para a primeira superfície:

s e n   θ 1 = n   s e n   θ 2

s e n   θ 2 = 1 n s e n   θ 1  

Vamos considerar o triângulo formado pelo vidro e o raio de luz, vemos que θ 3 = 90 ° - θ 2

Passo 2

Juntando todos esses resultados a condição para que haja reflexão interna total se torna:

1 ≤ s e n 90 ° - θ 2 = n cos ⁡ θ 2

Elevando esse resultado ao quadrado e usando a relação trigonométrica s e n 2 θ + c o s 2 θ = 1 :

1 ≤ n 2 s e n 2   θ 2

Mas como s e n   θ 2 = 1 n s e n   θ 1 , temos:

1 ≤ 1 - s e n 2 θ 1 n 2   = n 2 - s e n 2     θ 1

Passo 3

Portanto o maior valor para n no qual a desigualdade é verdadeira é aquele para o qual:

1 = n 2 - s e n 2   θ 1

Isolando n obtemos que:

n = 1 + s e n 2   θ 1 = 1 + s e n 2   ( 45 ) = 1,22

Resposta

O índice de refração do vidro é n = 1,22

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Prove que um raio de luz que incide em uma janela de vidro emerge do lado oposto com uma direção paralela à do raio original e um deslocamento lateral como na figura 33-69. (b) Mostre que, para pe
Na figura 33-71, dois raios luminosos que se estavam se propagando no ar passam por cinco placas de plástico transparente e voltam para o ar. As placas tem interfaces paralelas e espessura desconhecid
A Fig.35-56 mostra uma fibra ótica na qual um núcleo central de plástico, com um índice de refração n 1 = 1,58 , é envolvida por um revestimento de plástico com um índice de refração n 2 = 1,53 . Os r
A Fig.35-57 mostra um jogo de fliperama que foi lançado no Texas. Quando pistolas de lasers são apontadas para o centro de um conjunto de placas de plástico, onde se encontra o alvo, um tatu de barro.