Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 33.Problemas Adicionais - Ex. 79

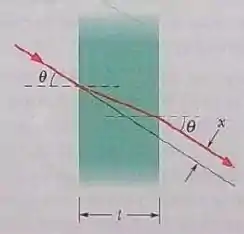
(a) Prove que um raio de luz que incide em uma janela de vidro emerge do lado oposto com uma direção paralela à do raio original e um deslocamento lateral como na figura 33-69. (b) Mostre que, para pequenos ângulos de incidência, o deslocamento lateral é dado por

x = t θ n - 1 n

em que t é a espessura do vidro, θ é o ângulo de incidência do raio em radianos e n é o índice de refração do vidro.

Passo 1

a)Temos que θ é o ângulo de incidência do raio de luz, o ângulo θ 2 é o ângulo de refração da primeira superfície do vidro.

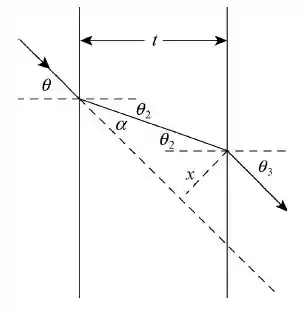
Considerando o n do ar aproximadamente 1, dessa primeira parte a lei de Snell é:

s e n θ 1 = n   s e n   θ 2

O ângulo de incidência na segunda parte da superfície é θ 2 e o ângulo de refração é θ 3 . Pela lei de Snell temos:

s e n θ 3 = n   s e n   θ 2

Logo temos que θ = θ 3 .

Podemos assim perceber que o raio incidente será paralelo ao raio que sai do vidro sofrendo apenas um deslocamento lateral.

Passo 2

b) Para obter a expressão de x como mostrado na figura, consideramos que d é a distânci percorrida pelo raio dentro do vidro, então:

d cos ⁡ θ 2 = t

Temos que o ângulo α = θ - θ 2 , então:

x = d   s e n   α = d   s e n   ( θ - θ 2 )

x = t s e n   ( θ - θ 2 ) cos ⁡ θ 2

Considerando pequenso ângulos, temos que s e n   θ - θ 2 ≈ θ - θ 2 e cos ⁡ θ 2 ≈ 1 , desta forma x fica:

x = t θ - θ 2 1 = t θ - θ n

x = t θ n - 1 n

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 35-33, um raio luminoso incide com um ângulo θ 1 = 50 ° em uma série de cinco placas transparentes com interfaces paralelas. Para as placas 1 e 3, L 1 = 20 μ m , L 3 = 25 μ m , n 1 = 1,6 e n 3
No modelo simplificado de fibra ótica discutido na Seç. 2.4 (cilindro circular de vidro), calcule o ângulo de incidência θ máximo na face de entrada (fig.) para o qual a luz será guiada dentro da fibr
Quando um raio de sol penetra numa gota de água, ele sofre reflexões múltiplas internas acompanhadas de transmissões parciais para fora. Considere um raio A B C D E que sofre uma única reflexão intern
• Uma estudante de física jogando bilhar deseja atingir a bola branca de forma que ela atinja a tabela e, então, a bola oito diretamente. Ela escolhe vários pontos na tabela e, então, mede a distância
Na Fig. 33-78, em que n 1=1,70 ,n 2 = 1,50 e n 3 = 1,30 , a luzé refratada do material 1 para o material 2. Se a luz incide no ponto A com o ângulo crítico da interface dos materiais 2 e 3, determine