Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 35.Problemas - Ex. 47
(a) Na figura 35.3, suponha que a fonte não estja em fase com , porém exista uma diferença de fase de meio ciclo. Para essa situação, a equação (35.1) fornece a condção para interferência destrutiva, e a equação (35.2) dá as condições para a interferência construtiva. Explique por quê. (b) Suponha que a fonte esteja uma fase adiantada em relação a : ou seja, se o deslocamento da fonte for , então, o deslocamento da fonte será . (No caso do item (a), .) Obtenha as fórmulas par as diferenças de caminhos que correspondam à interferência destrutiva e à interferência construtiva.
Passo 1
No caso que aparece na figura que o enunciado menciona, as duas ondas são geradas em fase.
Nessa situação, você precisa de uma “diferença de caminho” pra gerar interferência:
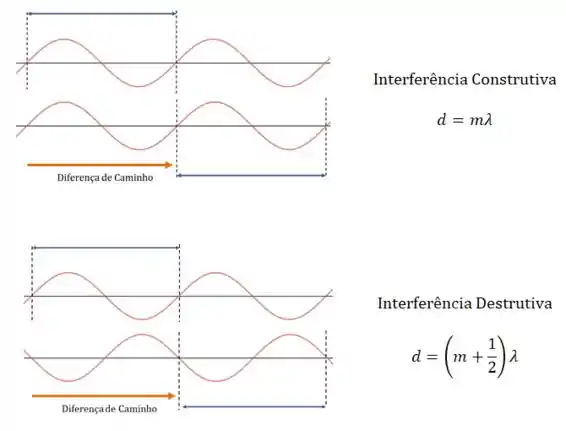
E o que acontece quando as ondas começam defasadas?
Passo 2
(a) Quando temos defasagem, é como se as ondas já começassem com uma diferença de caminho!
No caso do enunciado, como , essa diferença é de meio comprimento de onda.
Então, para chegar a uma diferença de um comprimento de onda (interferência construtiva), você vai ter que “completar” esse meio comprimento:
E para interferência destrutiva, você vai ter que manter a mesma situação, ou aumentar a diferença por comprimentos de onda inteiros:
Ou seja, as duas fórmulas se invertem!
Passo 3
(b) Em primeiro lugar, a gente precisa traduzir a diferença de fase em uma fração de comprimentos de onda.
Uma diferença de equivale a meio comprimento de onda, uma diferença de equivale a um comprimento inteiro! Então a fórmula geral é:
Ou seja, para ter interferência construtiva, a fórmula vai ter que mudar desse jeito:
E para interferência destrutiva:
Resposta
(a) A diferença de fase age como uma “diferença de caminho” inicial, que inverte as fórmulas para interferência construtiva e destrutiva.
(b) Para interferência construtiva , e para interferência destrutiva .