A figura abaixo mostra um quadrupolo elétrico formado por dois dipolos de mesmo módulo e sentidos opostos. Mostre que o valor de E em um ponto P do eixo do quadrupolo situado a uma distância z do centro (supondo) é dado por
em que Q () é chamado de momento quadrupolar da distribuição de cargas.
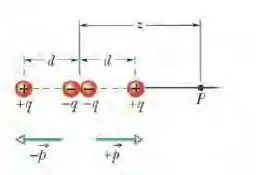
Passo 1
Olhando para a figura acima, podemos pensar em dois dipolos, cada um com um momento dipolar de módulo que conhecemos como:
Repare que os momentos que apontam na direção do eixo do quadrupolo, estão em sentidos opostos, o primeiro dipolo aponta para esquerda e o segundo dipolo aponta para direita). Tome como positivo o sentido para a direita.
Aqui usaremos o conceito de campo elétrico produzido por um dipolo e como temos dois dipolos vamos ter que combinar esse efeito depois, ok?
Passo 2
Vamos relembrar que o campo produzido por um dipolo é igual a:
Onde é a distância entre o ponto onde queremos calcular o campo elétrico e o centro do dipolo causador do campo.
Assim, o campo produzido pelo dipolo da direita é
Veja que a distância foi substituída pela equação:
E o campo produzido pelo dipolo da esquerda é:
Lembrando que colocamos como negativo, pois o momento dipolo aponta para esquerda e nós dissemos que nossa convenção é que todo momento dipolo que aponta para a esquerda é negativo!
Veja que nesse caso a distância entre o centro do dipolo e o local onde queremos calcular o campo elétrico é maior e foi substituída pela equação:
Passo 3
Logo o campo elétrico gerado pelos dois dipolos elétricos é igual a soma dos campos elétricos causados por cada dipolo elétrico:
Colocando em evidência alguns termos:
Como podemos usar as expressões binominais de aproximação, e elas serão muito necessárias pra chegarmos no formato que o enunciado pede.
E
Sei que isso pode assustar um pouco galera, mas fiquem tranquilos geralmente essas substituições são dadas não precisa decorar isso não, tá?
Passo 4
Temos essa equação do campo:
E agora vamos substituir aquelas aproximações:
Rearrumando essa galerinha pra deixar uma carinha bonitinha temos:
E vamos rearrumar mais um pouco, não desiste não!
Agora substituindo o nosso momento quadrupolar na expressão...
Encontramos o campo total segundo o enunciado!
Resposta
Ei, a resposta está no passo a passo :)