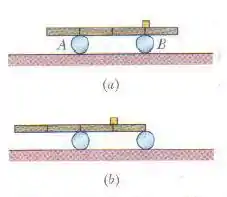
Na figura de cima uma viga homogênea de repousa simetricamente em dois rolamentos. As distâncias entre as marcas verticais ao longo da viga são iguais. Duas das marcas coincidem com a posição dos rolamentos; um pacote de é colocado sobre a viga, na posição do rolamento , Qual é o módulo da força exercida sobre a viga (a) pelo rolamento e (b) pelo rolamento ? A viga é empurrada para a esquerda até que a extremidade direita esteja acima do rolamento B(figura de baixo). Qual é o novo módulo da força exercida sobre a viga (c) pelo rolamento e (d) pelo rolamento ? A viga é empurrada para a direita. Suponha que tem um comprimento de m. (e) Que distância horizontal entre o pacote e o rolamento coloca a viga na iminência de perder contato com o rolamento ?
Passo 1
Vamos organizar as informações: temos uma viga de massa e um comprimento . O pacote que é colocado inicialmente sobre o rolamento tem massa .
A letra (a) quer saber qual o módulo da força exercida pela viga sobre o rolamento . Como está tudo em equilíbrio, e o enunciado diz explicitamente que a viga repousa simetricamente nos rolamentos, a força sobre o rolamento vai ser simplesmente a metade do peso da viga:
Passo 2
Seguindo a mesma lógica do item (a), o item (b) vai ser a mesma coisa, mas adicionando o peso do pacote:
Beleza, até aqui tudo tranquilo, porque tudo é simétrico. Mas as coisas mudam um pouco quando quebramos essa simetria.
Passo 3
(c) Agora queremos calcular o novo módulo da força que o rolamento exerce sobre a viga.
A situação “nova” é a seguinte, o centro de massa da viga está exatamente acima do centro de massa do rolamento .
E o centro de massa do pacote está sobre a viga, mas exatamente no meio do caminho entre e B.
Ou seja, a nova força vai ser:
Veja que legal, é simplesmente o contrário da situação anterior, agora a viga está toda sobre o e o pacote está dividido.
Passo 4
E você provavelmente já imagina o que vai acontecer na letra (d).
No equilíbrio, a única força que o rolamento exerce sobre a viga corresponde à metade do peso do pacote, porque o peso da viga em si está concentrado sobre o rolamento .
Então a força vai ser:
Passo 5
Agora pra fechar queremos saber o seguinte. Vamos empurrar a viga para a direita novamente: feito isso, a qual distância do rolamento queremos colocar o pacote para a viga ficar na iminência de perder o contato com o rolamento .
Vamos escrever a soma dos torques, colocando o rolamento como referência. Como a viga vai estar na iminência de perder o contato com o rolamento , ele não deve exercer nenhuma força sobre a viga:
Isolando a distância e cortando :
Substituindo os valores:
Pronto!
Resposta
(a)
(b)
(c)
(d)
(e)