Enunciado
Física - Halliday - Vol 3- Ed: 8º - Capítulo 25.4 - Ex. 13
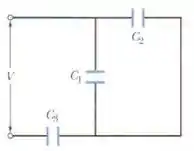
Na figura, uma diferença de potencial V = 100,0 V é aplicada ao circuito e os valores das capacitâncias são = 10,0 μF, = 5,00 μF e = 4,00 μF. Se o capacitor 3 sofre uma ruptura dielétrica e passa a se comportar como um condutor, determine
(a) o aumento da carga do capacitor 1;
(b) o aumento da diferença de potencial entre as placas do capacitor 1.
Passo 1
E aí! tudo certinho? 😉
Na figura, temos um circuito com três capacitores: , e . Uma diferença de potencial é aplicada ao circuito. Os valores das capacitâncias são: , e
Agora, vamos analisar o que acontece quando o capacitor 3 sofre uma ruptura dielétrica e passa a se comportar como um condutor:
Aumento da carga do capacitor 1 ():
Quando o capacitor 3 se torna um condutor, ele permite que a carga flua entre as placas. Como a carga total no circuito é conservada, a carga do capacitor 1 aumenta. A carga extra que estava no capacitor 3 agora é distribuída entre os outros capacitores.
Aumento da diferença de potencial entre as placas do capacitor 1:
A diferença de potencial entre as placas do capacitor 1 aumenta porque a carga total no circuito permanece a mesma, mas agora está concentrada em menos capacitores (já que o capacitor 3 se tornou um condutor). Portanto, a tensão entre as placas do capacitor 1 aumenta.
Vamos começar calculando a capacitância equivalente antes da ruptura:
Veja só! 😉
Passo 2
e estão em paralelo e eles estão em série com , então fica assim:
Substituindo os valores de , e ...
Agora podemos nos livrar de . O circuito fica assim:
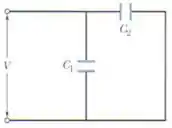
Tranquilo até aqui? 🤔
Passo 3
Vamos calcular o potencial de antes da ruptura.
é a capacitância equivalente depois de , ou seja, . (estamos basicamente aplicando o método de divisor de tensão...)
Substitua os valores:
Vamos responder a (b) primeiro. A tensão em 1 era de , e agora é já que a fonte de está ligada diretamente no capacitor . Então:
Legal, né? 😁
Passo 4
Agora vamos para a letra (a):
Agora é substituir os valores:
E aí! entendeu tudo? Responde Aí! 😉
Resposta
Letra (a):
Letra (b):