Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 16.Problemas Adicionais - Ex. 94
A figura mostra um anel circular, feito de corda, que gira em torno do ponto central em um local em que a gravidade é desprezível. O raio de anel é e a velocidade tangencial de um elemento da corda é . A corda é posta para vibrar na direção radial. Com que velocidade as ondas transversais se propagam ao longo do anel? (Sugestão: Aplique a segunda lei de Newton a um segmento pequeno, mas finito, da corda.)
Passo 1
Nosso objetivo é calcular a velocidade de propagação da onda na corda, que segue a seguinte fórmula:
Precisamos encontrar uma expressão para para poder calcular essa velocidade.
Vamos olhar para um pequeno trecho de corda em círculo e analisar as forças que agem sobre ele:
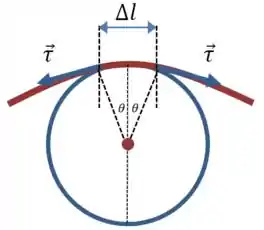
A componente da força restauradora que puxa a corda para o centro do círculo é:
E podemos aproximar esse seno:
Então:
Passo 2
E já que essa é a única força agindo na direção radial, ela deve cumprir o papel de força centrípeta que mantém a corda no formato circular:
Onde é a velocidade tangencial do trecho . E qual é a massa de um trecho de corda com comprimento ?
Onde é a densidade linear da corda. Então:
Substituindo isso na fórmula com que começamos o primeiro passo:
Ou seja, a velocidade da onda é igual à :
Resposta
As ondas transversais se propagam com .