Exercícios de Velocidade e Potência de uma Onda na Corda - Lista de Exercícios Resolvida
Questão 1
Uma corda na qual ondas podem se propagar tem m de comprimento e de massa. A tensão da corda é N. Qual deve ser a frequência de ondas progressivas com uma amplitude de mm para que a potência média seja ?
Ver solução completaQuestão 2
Qual é a velocidade de uma onda transversal em uma corda de de comprimento e g de massa sujeita a uma tensão de
Ver solução completaQuestão 3
A tensão num fio preso em ambos os extremos é duplicada sem que haja qualquer mudança considerável em seu comprimento. Qual é a razão entre as velocidades das ondas transversais nesse fio, antes e depois do aumento de tensão?
Questão 4
Uma onda transversal senoidal se propaga em uma corda no sentido negativo do eixo . A Figura abaixo mostra o deslocamento em função da posição no instante . A tensão na corda é e a massa específica linear . Assuma que a onda é da forma .
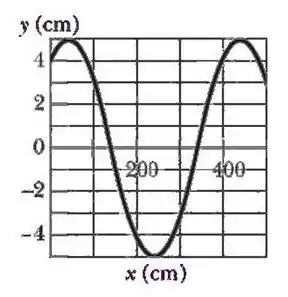
Determine a amplitude.
Encontre a velocidade da onda e a frequência da onda.
Calcule a taxa média de transporte de energia.
Ver solução completaQuestão 5
Energia é transmitida a uma taxa por uma onda de frequência em uma corda sob tensão . Qual é a nova taxa de transmissão de energia em termos de
- Se a tensão é aumentada para ?
- Se, em vez disso, a frequência é reduzida para ?
Questão 6
Uma corda uniforme de massa e comprimento está pendurada em um teto.
Mostre que a velocidade de uma onda transversal na corda é função de, a distância da extremidade inferior, e é dada por
Ver solução completaQuestão 7
A densidade linear de uma corda é . Uma onda transversal na corda é descrita pela equação:
Na qual e são expressos em metros e em segundos. Determine:
A velocidade de propagação da onda.
A tensão na corda.
Ver solução completaQuestão 8
Complete a seguinte afirmação: a potência emitida isotropicamente de uma onda sonora...
a) é inversamente proporcional ao quadrado da distância à fonte;
b) é proporcional ao quadrado da distância à fonte;
c) é inversamente proporcional ao quadrado da amplitude da onda;
d) é proporcional à distância à fonte;
e) nenhuma das alternativas;
Ver solução completaQuestão 9
Uma onda propaga-se numa corda na direção em sentido negativo com velocidade de . A tração na corda é de . A expressão do deslocamento dos pontos da corda em função do tempo é:
No instante os deslocamentos ao longo de são dados pelo gráfico abaixo.
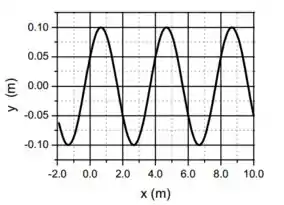
- Determine a amplitude do deslocamento e o comprimento de onda.
- Determine o ângulo de fase .
- Calcule e (deixe em função de e escreva a função para essa onda, escolhendo corretamente o sinal na frente de
- Obtenha e velocidade transversal dos pontos da corda em função de e
- Calcule a energia média por unidade de tempo transmitida pela corda.
Questão 10
Considere uma corda sujeita a uma tensão sobre a qual se encontra uma formiga em . A massa da formiga é muito menor que a massa do segmento da corda em que ela se encontra. Uma onda harmônica: é gerada na corda.
- Calcule a velocidade da formiga.
- Calcule a potência instantânea da onda a partir da sua definição.
- Determine o valor máximo da amplitude da onda para que a formiga permaneça presa a corda em qualquer instante de tempo( desconsidere a força com que a formiga se agarra a corda).
- Deduza a relação entre a velocidade da onda, o número de onda e a sua frequência angular.
Questão 11
O gráfico representa, num dado instante, a velocidade transversal dos pontos de uma corda, na qual se propaga uma onda senoidal na direção positiva do eixo dos .
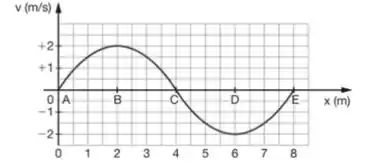
A velocidade de propagação da onda é de 24 m/s. Sejam A, B, C, D e E pontos da corda. Considere, para o instante representado, as seguintes afirmações:
A frequência da onda é
Os pontos A, C e E têm máxima aceleração transversal (em módulo)
Os pontos A, C e E têm máximo deslocamento transversal (em módulo)
Todos os pontos da corda se deslocam com velocidade de 24 m/s na direção do eixo .
Estão corretas:
- Todas
- Somente IV
- Somente II e III
- Somente I e II
- Somente II, III e IV
Questão 12
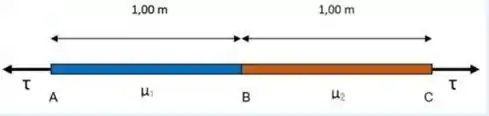
Uma fonte vibratória produz uma onda transversal periódica, que se propaga com velocidade , numa corda AB, cuja densidade linear de massa é , conforme mostra a figura. Essa corda está ligada a uma outra, BC, cuja densidade linear de massa é . Para a onda que se propaga na corda BC, qual é seu comprimento de onda?
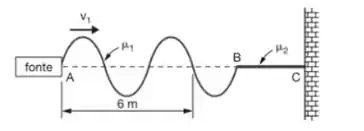
Questão 13
A velocidade dos pulsos em uma corda, presa no teto, que sustenta um peso vale. O que acontece com a velocidade de propagação dos pulsos se um segundo peso for fixado no primeiro peso, sem que a corda seja distendida?
- Ela adquire o valor 2
- Ela adquire o valor
- Ela adquire o valor.
- Ela adquire o valor .
- Ela adquire o valor
Questão 14
Uma onda transversal viajando ao longo de uma corda transporta energia a uma taxa P. Se quiséssemos dobrar essa taxa, deveríamos:
- Aumentar a amplitude da onda por um fator de 8.
- Aumentar a amplitude da onda por um fator de quatro.
- Aumentar a amplitude da onda por um fator de dois.
- Aumentar a amplitude por um fator de .
Questão 15
Uma corda de densidade linear é esticada sob uma tensão de . A corda tem de comprimento e ,simultaneamente, a partir de cada uma das extremidades, introduzem-se oscilações de frequências iguais a , e de mesma amplitude Depois de quantos segundos elas se encontram?
Questão 16
Uma onda senoidal se propaga em uma corda de massa específica linear . A onda é descrita por , com dado em metros e em segundos. Determine o período de oscilação e a tensão na corda .
Questão 17
Na figura abaixo, qual e a curva que melhor representa o comportamento da velocidade da onda em uma corda com a tensão na corda?
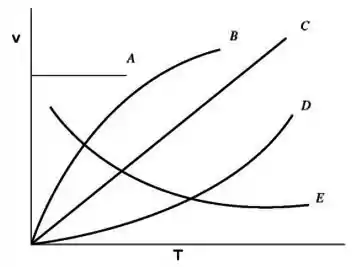
- A
- B
- C
- D
- E
Questão 18
. Uma corda tem massa e comprimento . Ela vibra num modo normal descrito pela função de onda
com em metros e em segundos. Determine:
O comprimento de onda desta onda.
Diga se os extremos e estão fixos ou livres para oscilar.
A frequência de vibração de cada ponto da corda.
A tensão a qual a corda está submetida.
A velocidade transversal máxima de um ponto da corda localizado num ventre.
Se necessário, a resposta pode ficar em função de .
Ver solução completaQuestão 19
8 - Um aluno prende um pedaço de linha de pesca de nylon a um poste. Ela a estica e sacode a extremidade da corda na mão para cima e para baixo para produzir ondas na linha. Se o aluno quiser aumentar o máximo possível o comprimento da onda, ele deve
- aumentar a tensão na corda e agitar a extremidade mais vezes por segundo
- diminuir a tensão na corda e agitar a extremidade mais vezes por segundo
- aumentar a tensão na corda e agitar a extremidade menos vezes por segundo
- diminuir a tensão na corda e agitar a extremidade menos vezes por segundo
- manter a tensão e a frequência iguais, mas aumentar o comprimento da corda
Questão 20
Uma onda harmônica se propaga em uma corda fazendo a corda oscilar na direção . A massa específica linear da corda é . Os deslocamentos da corda nas posições e variam com o tempo de acordo com as seguintes equações:
Onde o tempo está em segundos, ao passo que estão em centímetros.
- Quais são a amplitude e o período dessa onda harmônica?
- Se for o valor do comprimento de onda em metros, qual será a tensão na corda em termos de ?
- Qual é o maior comprimento de onda compatível com os dados do enunciado?
Dica: Note que a função pode ser equivalentemente escrita como para qualquer número inteiro , ou seja, uma fase de pode ter sido omitida no enunciado. Por isso, há vários valores possíveis para o número de onda angular.
Ver solução completaQuestão 21
As fórmulas matemáticas para três ondas que se propagam em uma corda são dadas por: Onda 1:
Onda 2:
onde é dado em metros e em segundos. Responda das ondas acima quais tem respectivamente a maior velocidade de propagação e a maior velocidade transversal
Ver solução completaQuestão 22
Duas cordas foram amarradas uma na outra com um no e depois esticadas entre 2 suportes rígidos, conforme a figura abaixo. As cordas têm densidades lineares e . Seus comprimentos são e . A tensao e a mesma em ambas as cordas e vale . Simultaneamente, um pulso e enviado a partir da extremidade rígida de cada corda em direção ao nó. O tempo para cada pulso chegar ao nó será:
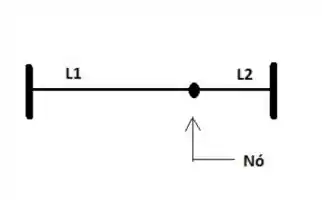
- Não é possível determinar os tempos sem conhecer a frequência das ondas nas cordas
Questão 23
Uma onda transversal se propaga em uma corda de massa m e comprimento L. Se a força de
tração aplicada à corda é T, qual das afirmações abaixo em relação à onda é verdadeira?
a) a velocidade da onda depende apenas de m, L;
b) o comprimento de onda da onda depende apenas de L;
c) o comprimento de onda da onda depende apenas de m, L e T;
d) a velocidade da onda depende de m, L e T;
e) tanto a afirmação a) quanto a afirmação d) são verdadeiras;
Ver solução completaQuestão 24
O deslocamento de uma corda na qual existe uma onda senoidal progressiva é dado por
. Se no instante , o ponto localizado em tem velocidade e deslocamento , o valor da constante de fase é dado por
a) ;
b) ;
c) ;
d) ;
e) ;
Ver solução completaQuestão 25
Ao tocar uma corda do seu violão no seu modo fundamental, um músico percebe que o som produzido está desafinado. Se ele gira a tarracha do violão de modo a apertar mais a corda, o que acontece com as ondas sonoras produzidas?
A) A velocidade das ondas sonoras aumenta, o seu comprimento de onda não muda e a nota produzida fica mais aguda
B) A velocidade das ondas sonoras aumenta, o seu comprimento de onda aumenta e a nota produzida fica mais grave
C) A velocidade das ondas sonoras não muda, o seu comprimento de onda aumenta e a nota produzida fica mais grave
D) A velocidade das ondas sonoras não muda, o seu comprimento de onda cai e a nota produzida fica mais aguda
E) A velocidade das ondas sonoras aumenta, o seu comprimento de onda cai e a nota produzida fica mais aguda
Ver solução completaQuestão 26
Uma onda senoidal é gerada numa corda e se propaga no sentido positivo de x com frequência de 20 Hz. A amplitude da onda é de 2 mm e o deslocamento inicial da corda é igual a metade desse valor. A tensão aplicada à corda vale 10 N e a densidade linear de massa vale 0,1 kg/m. Calcule:
a) A velocidade de propagação da onda na corda;
b) O comprimento de onda;
c) A constante de fase;
d) Escreva a equação do movimento da corda, explicitando todos os valores numéricos;
e) Calcule a velocidade transversal da corda para t = 0 s em x = 0 m. Use e .
Ver solução completaQuestão 27
Como mostrado na figura, uma onda senoidal se propaga para a direita com velocidade v1 ao longo da corda 1, que tem uma densidade linear de massa μ1. Esta onda tem uma frequência f1 e um comprimento de onda λ1. Como a corda 1 está presa à corda 2 (que tem densidade linear de massa μ2= 3μ1), a primeira onda excitará uma nova onda na corda 2, que também se propaga para a direita. Qual é a velocidade v2 da onda produzida na corda 2?
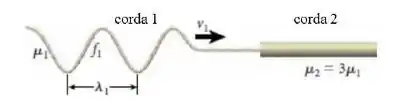
a) ;
b) ;
c) ;
d);
e) ;
Ver solução completaQuestão 28
Marque a afirmação INCORRETA a respeito do comportamento da oscilação de uma corda. Aqui, são frequência angular, número de onda, comprimento de onda e período, respectivamente.
- A velocidade da onda aumenta se a densidade linear da corda diminuir.
- A frequência é proporcional a
- A densidade de energia é proporcional à amplitude.
- A velocidade da fase é dada por .
- A velocidade da fase é dada por
Questão 29
Uma corda de massa m e comprimento L está suspensa verticalmente com um corpo de massa M preso na extremidade inferior da corda.
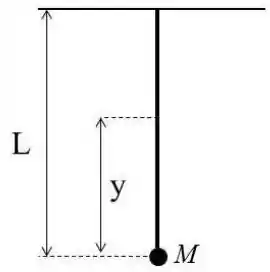
a) Calcule a velocidade de uma onda transversal na corda em função de y, a distância da extremidade inferior.
b) Calcule o tempo para uma onda transversal percorrer o comprimento da corda.
Ver solução completaQuestão 30
Considere uma corda de comprimento e densidade , presa nas duas extremidades.
- Qual é, em newtons, o valor da tensão que deve ser aplicada na corda para que seu primeiro harmônico ocorra em ?
- Suponha que uma extremidade da corda está em e a outra . A onda do item (a) pode ser descrita como . Para cm, determine, em , a velocidade máxima de um ponto no meio da corda.
Dados:
Ver solução completaQuestão 31
Considere uma corda de comprimento e densidade , presa nas duas extremidades.
- Qual é, em newtons, o valor da tensão que deve ser aplicada na corda para que seu primeiro harmônico ocorra em ?
- Suponha que uma extremidade da corda está em e a outra em . A onda do item (a) pode ser descrita como . Para , determine em a velocidade máxima de um ponto no meio da corda.
Dado:
Ver solução completaQuestão 32
A figura ao lado mostra dois gráficos que representam uma onda transversal em uma corda de de massa e de comprimento, descrita por uma função . A onda está se movendo no sentido positivo de . Com base nesses dados e na informação contida nesses gráficos, determine:
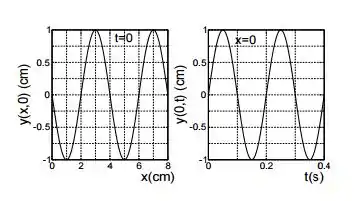
Obs: justifique todas as respostas
- A amplitude e frequência da onda.
- O comprimento de onda e a velocidade da onda.
- A expressão que descreve a onda.
- A tensão na corda.
Questão 33
Uma certa onda transversal com amplitude e frequência transfere energia em uma corda a uma taxa média . Se a amplitude e a frequência são dobradas, a nova onda transferirá energia a uma taxa média de:
Questão 34
Uma onda transversal senoidal se propaga em uma corda no sentido negativo do eixo . A Figura abaixo mostra o deslocamento em função da posição no instante . A tensão na corda é e a massa específica linear . Assuma que a onda é da forma .
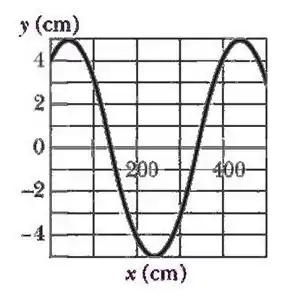
Determine a amplitude e o comprimento de onda.
Encontre a velocidade da onda, o período e o sinal que precede .
Determine a velocidade transversal máxima de uma partícula da corda.
Determine a constante de fase .
Calcule a taxa média de transporte de energia.
Ver solução completaQuestão 35
12 - Na figura está representada a configuração de uma onda mecânica que se propaga com velocidade de .
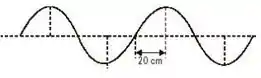
A frequência desta onda vale:
Questão 36
Uma corda de violino tem comprimento de e está afinada na nota sol, .
A que distância da extremidade se deve apertar a corda para que soe como um lá, ?
Se o violinista quisesse afinar essa mesma corda em lá, que variação relativa de tração ele deveria fornecer?
Ver solução completaQuestão 37
Qual a velocidade de escape de um próton que se encontra sob a superfície de uma esfera condutora de potencial ? (Considere no infinito).
Ver solução completaQuestão 38
Uma onda senoidal monocromática se propaga em um trecho de uma corda em que essa é uniforme. A corda, disposta horizontalmente, apresenta, no entanto, um segundo trecho em que a sua densidade linear é uniforme, mas diferente da inicial. A tensão na corda é a mesma ao longo dela toda. As figuras a seguir representam fotografias da corda no primeiro trecho (superior) e no segundo trecho (inferior).
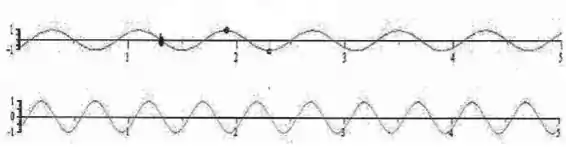
As figuras foram construídas com escalas verticais distintas e muito exageradas, mas com a mesma escala horizontal. Justifique cada resposta.
A frequência de onda é a mesma nos dois trechos?
O comprimento de onda é o mesmo nos dois trechos?
Qual trecho apresenta densidade linear maior?
Indique na figura a direção e o sentido da velocidade instantânea do ponto material da corda indicado na figura. Indique também um ponto cuja velocidade instantânea seja igual a zero
Ver solução completaQuestão 39
. Um fio muito longo é feito juntando-se outros dois fios com densidades lineares diferentes e a junção dos fios pode ser localizada no ponto . A figura abaixo mostra uma porção do fio, centrada na junção. O fio é esticado sob uma tensão . No instante , é produzido um pequeno pulso transversal, localizado no ponto . Considere as distâncias indicadas na figura abaixo. Em que instante de tempo o pulso atinge o ponto ?
.
.
.
.
.
Ver solução completaQuestão 40
. Escreva uma expressão que descreva a variação de pressão em função da posição e do tempo para uma onda sonora no ar, sendo o deslocamento dos elementos de ar, e . Considere a velocidade do som .
.
.
.
.
.
Ver solução completaQuestão 41
Uma corda esticada com de comprimento e de massa sofre uma tensão de . Qual deve ser a frequência de uma onda progressiva que se propaga nesta corda com amplitude de tendo potência média de ? (Considere ).
Ver solução completaQuestão 42
Uma onda transversal senoidal está viajando em uma corda. Qualquer ponto na corda:
- se move com velocidade constante na mesma direção da onda
- se move em movimento harmônico simples com uma frequência diferente da frequência da onda
- se move em movimento harmônico simples com a mesma frequência da onda
- se move em movimento circular uniforme com frequência diferente da frequência da onda
- se move em movimento circular uniforme com a mesma velocidade angular que a da onda
Questão 43
Os itens são independentes. Indique a resposta com o número de algarismos significativos adequados.
a) Uma onda senoidal com período se propaga em uma corda. Sabendo que, para dois pontos da corda separados por , a diferença de fase é de , determine a velocidade da onda na corda.
b) A equação que descreve uma onda transversal em uma corda é . Sabendo que esta onda ao se refletir em um anteparo produz um padrão estacionário para o segundo harmônico em uma corda com comprimento , determine a velocidade da onda.
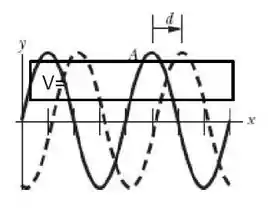
c) A figura mostra dois instantes (linha contínua) e (linha tracejada) de uma onda que se propaga em uma corda. Sabendo que a distância d é igual a , que e a frequência angular é determine a velocidade da onda.
Questão 44
Uma corda de material homogêneo, de 20 m de comprimento e massa de 2 kg está esticada sob uma tensão de 10 N.
(a) Faz-se oscilar transversalmente uma extremidade da corda, com amplitude de 3 cm e frequência de 5 oscilações por segundo. A posição vertical inicial desta extremidade em t = 0 é 1,5 cm para cima. Escreva, como função do tempo, o deslocamento vertical de um ponto situado à distância x da extremidade que se faz oscilar, após ser atingido pela onda mas antes de que a mesma chegue à outra extremidade. Deixe também explícito qual é a velocidade v de propagação da onda progressiva.
Ver solução completaQuestão 45
4 - Uma corda de guitarra possui atualmente uma frequência fundamental de . Que porcentagem de aumento de tensão é necessária se quisermos reajustar essa frequência fundamental para ?
Questão 46
13 - Considere uma pessoa batendo periodicamente em um ponto da superfície de um líquido. Uma onda passa a se propagar nessa superfície. Considere as seguintes afirmações:
I) A velocidade de propagação (v) da onda na superfície de um líquido depende do meio. Assim, em líquidos diferentes (água, óleo etc.) teremos velocidades de propagação diferentes.
II) A distância entre duas cristas sucessivas é o comprimento de onda λ.
III) A frequência f da onda é igual à frequência das batidas no líquido.
IV) Como v é constante para um determinado meio, quanto maior for f, menor será o valor de λ neste meio.
Assinale a alternativa correta:
- apenas as afirmativas I, II e IV são corretas.
- apenas as afirmativas I e III são corretas.
- apenas as afirmativas I, III e IV são corretas.
- apenas as afirmativas II e IV são corretas.
- todas as afirmativas estão corretas.
Questão 47
Um sistema massa-mola não amortecido é formado por um bloco de massa e por uma mola de constante elástica O sistema é submetido a uma força externa dada por
sendo
Sabendo que no instante , o bloco encontra-se em repouso, na posição , é correto afirmar que:
a)
b)
c)
d)
e) Nenhuma das demais alternativas.
Ver solução completaQuestão 48
Uma corda esticada está amarrada a uma parede distante. Uma demonstradora movimenta sua mão para criar um pulso se propagando em direção à parede (veja diagrama). A demonstradora quer produzir um pulso que leve um tempo maior para atingir a parede. Qual das ações devem ser feitas por ela para produzir esse resultado:

Usar uma corda mais pesada, de mesmo comprimento, sob a mesma tensão.
Usar uma corda de mesma densidade, mas aumentar a tensão.
Movimentar sua mão a uma distância maior, para cima e para baixo com a mesma quantidade de tempo.
Nenhuma das ações acima irá causar o efeito desejado.
Ver solução completaQuestão 49
Uma corda de massa especifica linear (ou, densidade linear de massa) é tensionada por uma força de tração. Ondas transversais são excitadas na corda e se propagam de acordo com a função senoidal
onde e são dados em metros e em segundos. Nestas condições, determine:
(a) O deslocamento transversal da corda quando e .
(b) O comprimento de onda
(c) O período .
(d) A velocidade de propagação da onda .
(e) A intensidade da força de tensão na corda.
(f) Se dobrarmos o valor da amplitude da onda dada pela função acima, de quanto aumenta a potência transmitida pela onda?
Ver solução completaQuestão 50
Considere duas cordas inextensíveis e homogêneas idênticas, sujeitas à mesma tensão. Em cada uma temos uma onda em um modo normal diferente. Considere as afirmações abaixo:
- As velocidades de propagação das ondas são diferentes.
- Os números de onda são iguais, mas as frequências diferentes.
- As frequências são iguais, mas os números de onda diferentes.
- As velocidades de propagação das ondas são iguais.
- Os números de onda e frequência são iguais
- Os números de onda e as frequências são diferentes.
Quais afirmações acima são verdadeiras?
- e
- e
- e
- e
- e
- e
- e
- e
Questão 51
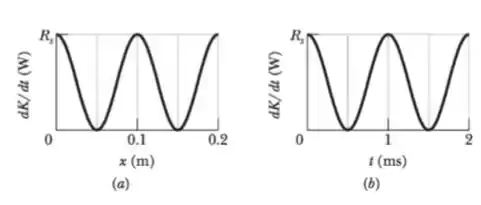
Uma onda senoidal é produzida em uma corda comum a densidade linear . Enquanto a onda se propaga, a energia cinética dos elementos de massa ao longo da corda varia. A Figura abaixo mostra, em um certo instante, a taxa de energia cinética em função da distância ao longo da corda. A Figura abaixo é semelhante, exceto pelo fato de que esta mostra a taxa em função do tempo para um dado elemento de massa situado em um certo ponto. Nos dois casos, a escala do eixo vertical é definida por . Qual é a amplitude da onda expressa em metros?
Ver solução completa
Questão 52
A tensão num fio preso em ambos os extremos é duplicada sem que haja qualquer mudança considerável em seu comprimento. Qual é a razão entre as velocidades das ondas transversais nesse fio, antes e depois do aumento de tensão?
Questão 53
As três ondas a seguir são produzidas em três cordas com a mesma massa específica linear (está em metros e em segundos):
;
= ()
Assinale a alternativa correta para a onda resultante:
.
Analise as proposições abaixo:
I – A tensão na corda 1 é maior que a tensão na corda 2.
II – A velocidade de propagação da onda na corda 1 é maior que a velocidade na corda 3.
III – A tensão na corda 2 é menor que a tensão na corda 3.
IV - A tensão na corda 3 é maior que a tensão na corda 1.
V – A velocidade de propagação da onda na corda 2 é maior que a velocidade na corda 1.
VI – A velocidade de propagação da onda na corda 2 é menor que a velocidade na corda 3.
Assinale a alternativa cujos itens estão corretos.
a) I, II e VI
b) I e V
c) III, V e VI
d) I eII e) IV, V e VI
f) II e IV
Ver solução completaQuestão 54
Uma onda que se propaga ao longo de uma corda ideal apresenta a velocidade de fase ( ) igual à velocidade de grupo (). Porém, quando se considera uma corda real, a dependência da frequência angular com o número de onda pode ser descrita pela relação de dispersão:
onde é uma constante positiva que depende das propriedades mecânicas da corda e é a tensão aplicada na corda de densidade linear de massa . Se a razão entre a velocidade de fase e a velocidade de grupo é para uma onda com número de onda , para uma corda de densidade sujeita a uma tensão , o valor da constante , no sistema SI, é:
a) .
b) .
c) .
d).
e) .
f) .
g) nenhuma das respostas indicadas.
Ver solução completaQuestão 55
Uma onda transversal senoidal com um comprimento de onda de 80 cm propaga-se no sentido positivo de um eixo x. A figura abaixo mostra a velocidade transversal da partícula situada em x = 0 em função do tempo.
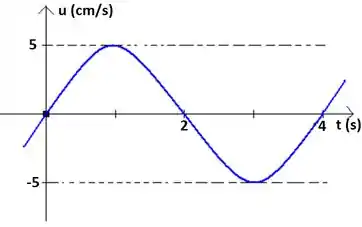
a) Determine a frequência e a velocidade de propagação da onda.
b) Determine a amplitude da onda (máximo deslocamento das partículas).
c) Determine a função de onda y(x,t) e faça o gráfico entre x = 0 e x = 80 cm no instante t = 2 s.
Considere agora que a onda acima se superponha a outra onda com a mesma frequência e mesma amplitude, mas com uma diferença de fase em relação a ela.
d) Encontre a diferença de fase para que a taxa média de energia transportada pela onda resultante seja o dobro da transportada por cada onda, separadamente.
Ver solução completaQuestão 56
O que se pode dizer sobre uma onda em uma corda cujas duas metades são de materiais e dimensões diferentes?
I. A velocidade de propagação deve ser a mesma nas duas metades.
II. A frequência deve ser igual nas duas metades.
III. O período deve ser igual nas duas metades.
IV. O comprimento de onda deve ser igual nas duas metades.
(a) Somente II e III.
(b) Somente II.
(c) Somente I e IV.
(d) Somente I.
(e) Somente IV.
(f) Somente I e II.
(g) Somente III e IV.
(h) Somente I, II e IV.
Ver solução completaQuestão 57
Uma onda progressiva transversal está se propagando numa corda infinita esticada. Escolhemos como eixo Ox a extensão da corda quando em repouso e o sentido da progressão como positivo. Seja Oy a direção da vibração da corda. São dadas a velocidade de propagação da onda, , e a densidade linear de massa da corda, . No instante , a forma da onda é dada por , onde , .
(a) Determine o comprimento de onda dessa onda e faça um esboço dessa onda para em , indicando as escalas escolhidas no eixo Ox e no eixo Oy.
(b) Determine o período T dessa onda e ache a expressão matemática do deslocamento transversal da corda em função de (x,t).
(c) Determine a magnitude da tensão F na corda.
(d) Calcule a partir da potência instantânea (em Watts) a potência média, em um período, transportada pela onda.
Ver solução completaQuestão 58
De que fator devemos modificar a tensão numa corda para duplicar o comprimento das ondas de uma dada frequência que nela se propagam?
- 2
- 1/2
- 4
- ¼
- 1/8
Questão 59
Uma fonte de vibração é colocada na extremidade de uma corda esticada fazendo com que o deslocamento vertical na extremidade () seja dado pela equação , onde é dado em metros e em segundos. A tensão na corda é de e a massa por unidade de comprimento é de . Considere que a corda seja longa o suficiente de modo que efeitos de interferência e reflexão de ondas na corda possam ser desprezados.
- Qual é a velocidade da onda gerada na corda?
- Qual é a frequência da onda?
- Qual é o comprimento de onda?
- Escreva, como função do tempo, o deslocamento transversal de um ponto da corda situado a uma distância à direita da extremidade ().
- Calcule a intensidade da onda progressiva gerada.