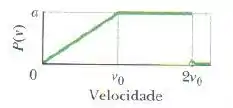
A figura mostra a distribuição de velocidades hipotética das partículas de um gás [note que para qualquer velocidade ]. Qual é o valor de (a) , (b) e (c) ? (d) Qual é a fração de partículas com velocidades entre e ?

Agora vamos dar uma olhada no gráfico. Qual é a equação daquela reta inclinada logo no início.

Como ela cruza a origem, já dá pra afirmar que a constante é zero. E o vai ser simplesmente a clássica variação do sobre variação do :

Ou seja, a equação daquela reta inclinada (entre o e ) é:

E na parte reta (entre e ), aí é só uma função constante:

(b) Agora a gente já tem a equação do gráfico, é só lembrar de algumas definições. Por exemplo, qual é relação da velocidade média com aquela integral lá de cima?

Beleza, agora ficamos com uma integral mais razoável. Mas integrar primeiro a parte da reta inclinada:

E a parte da função constante:

E somando as duas:

Como descobrimos antes que .

E então a resposta vai ser:

(c) Agora vamos fazer basicamente a mesma coisa, mas a definição da velocidade quadrática média:

Mais uma vez, começando pela parte da reta inclinada:

Beleza, agora somando as duas e substituindo por :

E então a resposta vai ser:

(d) A gente já viu que nesse gráfico a área está ligada ao número de partículas em uma determinada velocidade, certo?

E na letra (a) nós vimos que a área total embaixo do gráfico é . Então a fração das partículas entre e é:

E como a função é constante e igual a nesse intervalo inteiro:

Pronto!