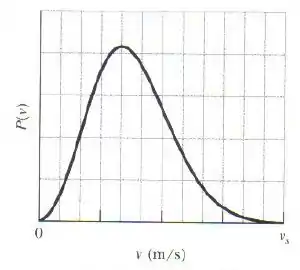
A figura mostra a distribuição de probabilidade da velocidades das moléculas de uma amostra de nitrogênio. A escala do eixo horizontal é definida por . Determine (a) a temperatura do gás e (b) a velocidade média quadrática das moléculas.

(a) Então beleza, o que é aquele pico do gráfico? É a velocidade mais provável para as moléculas! Mas essa fórmula a gente conhece:

Como aquele vale , cada “traço” do eixo horizontal vale , como o pico exatamente no quarto traço:

E pra isolar a temperatura vamos elevar tudo ao quadrado:

A questão não deu o valor de , mas falou que o gás é o nitrogênio , então podemos olhar uma tabelar pra saber que a massa molar é:

E então:

(b) E agora vamos lembrar a fórmula da velocidade média quadrática:

Bem parecida com a fórmula de antes né? Então vamos facilitar a vida:

Como essa segunda fórmula pode virar a primeira? Bom, a única diferença é que uma tem um dois na raiz e a outro tem um três, então é só fazer um “truque” simples pra transformar uma fórmula na outra:

Concorda? Então: