Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 19.6 - Ex. 41
Uma molécula de hidrogênio (diâmetro ), movendo-se à velocidade média quadrática, escapa de um forno a para uma câmara que contém átomos de argônio frios (diâmetro ) em uma concentração . (a) Qual é a velocidade da molécula de hidrogênio? (b) Qual é a distância mínima entre os centros para que a molécula de hidrogênio colida com um átomo de argônio, supondo que ambos são esféricos? (c) Qual é o número inicial de colisões por segundo que a molécula de hidrogênio sofre? (Sugestão: Suponha que os átomos de argônio estão parados. Nesse caso, o livre caminho médio da molécula de hidrogênio é dado pelas equações e não pela equação .)
Equação :
Passo 1
Ok, temos uma molécula de hidrogênio que acabou de sair de um forno onde a temperatura é:
A pergunta diz que ele se move com a velocidade média quadrática, e pede para calcularmos esse valor. A fórmula é:
E aí só fica faltando completar a massa molar da molécula de hidrogênio () que é:
E então:
Passo 2
(b) Agora temos que ter cuidado pra entender o que está sendo pedido: a distância mínima entre os centros para que haja uma colisão entre hidrogênio e argônio supondo que eles sejam esféricos.
Bom, em outras palavras: qual tem que ser a distância entre os centros para duas esferas colidirem?
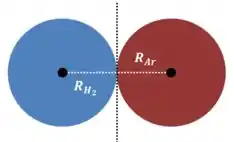
Exatamente, a distância entre os centros tem que ser igual à soma dos raios:
Como o enunciado deu os diâmetros, é só dividir os dois pela metade:
E essa é a resposta da letra (b).
Passo 3
(c) Agora vamos supor que os átomos de argônio estão parados.
A questão quer saber o seguinte: qual o número inicial (logo que o sai do forno) de colisões por segundo?
Bom, tem um jeito fácil de resolver isso. A questão disse que a concentração de argônio na câmara é .
Se a gente descobrir quantos centímetros cúbicos um átomo de hidrogênio “varre” por segundo, dá pra termos uma ideia de quantas colisões por segundo acontecem, olha só:
Então tá, vamos procurar esse valor. Imagine um átomo de hidrogênio de raio:
Andando com aquela velocidade:
Pelo resultado da letra (b), esse átomo colide com todos os átomos de argônio que tem um centro a uma distância .
Ou seja, a cada segundo, é como se o átomo varresse um cilindro de raio e altura :
Obs.: Convertemos a velocidade para centímetros por segundo, só pra resposta ficar em centímetros cúbicos, como queríamos no início.
Esse é o volume que o átomo varre em um segundo. Voltando na nossa lógica inicial:
E essa é a resposta da letra (c).
Resposta
(a) .
(b) .
(c) O hidrogênio colide com .