Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 20.6 - Ex. 41
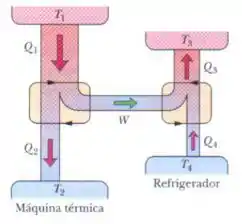
A figura mostra uma máquina de Carnot que trabalha entre as temperaturas e e alimenta um refrigerador de Carnot que trabalha entre as temperaturas e . Qual é a razão ?
Passo 1
Vamos começar lembrando das definições para a eficiência do motor e do refrigerador de Carnot.
Primeiro, pela própria definição de eficiência do motor, temos:
Mas, para o motor de Carnot, também vale a seguinte fórmula:
Segundo, a definição de eficiência do refrigerador é:
E para o refrigerador de Carnot, também vale:
E é igual para os dois, já que nesse caso o motor está alimentando o refrigerador. Então ficamos com o seguinte sistema de equações:
Passo 2
Pensando apenas em termos de conservação de energia, podemos encontrar expressões para :
Como nosso objetivo é calcular , vamos substituir essa última equação na primeira equação do nosso sistema:
Agora vamos isolar na segunda equação do sistema e substituir nessa última:
Então:
Passo 3
Agora vamos tentar usar essa última relação para calcular :
Por fim, vamos simplificar um pouco essa expressão:
Vamos dividir o numerador e o denominador por :
Passo 4
Agora vamos substituir os valores numéricos:
Resposta
A razão entre os calores é .