Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 20.4 - Ex. 45
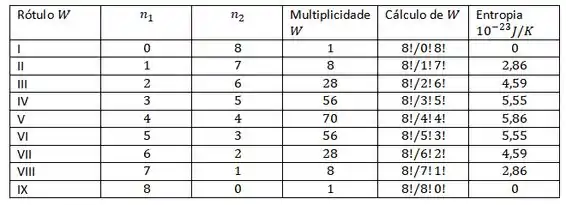
Construa uma tabela como a Tabela para oito moléculas
Passo 1
Olá pessoal, tudo bem? Vamos treinar um pouco de mecânica estatística? Bora lá?
Sabemos que para o caso de moléculas indistinguíveis, o número de multiplicidade de estados possíveis é dado por:
Onde o número total de partículas é conservado e dado por . Os índices correspondem às metades de uma caixa isolada onde o gás se encontra. A molécula pode estar tanto no lado , quanto no lado , mas sempre a soma de moléculas que estão nos dois lados vai ser a mesma e igual a . Ok? Beleza até aqui?
Para moléculas, temos e . Assim a multiplicidade fica:
As possíveis configurações vão ser dadas conforme for variando, de até .
Passo 2
A tabela também mostra valores de entropia associado a cada microestado. A equação da entropia de Boltzmann é:
Então, para cada configuração vamos ter um valor de entropia associado a ele.
Show!
Vamos agora calcular todos os casos de ?
Passo 3
- Para :
- Para :
- Para :
- Para :
- Para :
- Para :
- Para :
- Para :
- Para :
Faz sentido né? Pois só em uma configuração que todas as moléculas vão estar no lado .
E a entropia associada:
E a entropia associada:
Obs: lembrando que
E a entropia associada:
E a entropia associada:
E a entropia associada:
E a entropia associada:
E a entropia associada:
E a entropia associada:
E a entropia associada:
Agora que temos todos os dados, vamos colocar e forma de tabela?
Resposta
