Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 17.Problemas Adicionais - Ex. 71
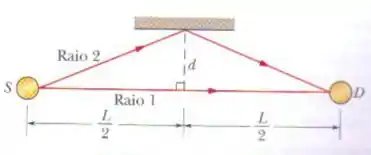
Na figura, um som de comprimento de onda é emitido isotropicamente por uma fonte pontual . O raio de som se propaga diretamente para o detector , situado a uma distância . O raio de som chega a após ser refletido em uma superfície plana. Essa reflexão ocorre sobre a mediatriz do segmento de reta , a uma distância do raio , Suponha que a reflexão desloca a fase da onda sonora de . Qual é o menor valor de (diferente de zero) para o qual o som direto e o som refletido chegam a (a) em oposição de fase e (b) em fase?
Passo 1
Vamos começar encontrando uma expressão geral para a diferença no caminho percorrido pelo cada um dos raios.
Podemos calcular a distância usando o teorema de Pitágoras:
E a distância pode ser encontrada diretamente a partir do desenho:
E o último termo da fórmula do é referente à defasagem gerada pela reflexão. Então ficamos com:
Passo 2
(a) No caso em que as duas ondas chegam até em oposição de fase, a diferença de caminho entre elas deve ser algum múltiplo inteiro de meio comprimento de onda:
Queremos que . Como estamos interessados no menor valor para , vamos começar considerando , então:
Mas o enunciado exigiu que seja diferente de zero, então vamos procurar o próximo valor, ou seja, .
Vamos substituir e :
Elevando os dois lados ao quadrado:
Passo 3
(b) Agora vamos fazer a mesma coisa, mas procurando casos em que a diferença de caminho é um múltiplo inteiro de um comprimento de onda.
Queremos que E mais uma vez vamos começar com o menor valor, .
Vamos substituir e :
Elevando os dois lados ao quadrado:
Resposta
(a) Para que as ondas cheguem em oposição de fase, o menor para é .
(b) Para que as ondas cheguem em fase, o menor valor para é .