Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 18.6 - Ex. 63
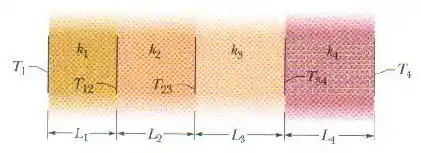
A figura mostra uma parede feita de quatro camadas, de condutividades térmicas , e ( não é conhecida). As espessuras das camadas são , e ( não é conhecida). As temperaturas conhecidas são , e . A transferência de energia está no regime estacionário. Qual é o valor da temperatura ?
Passo 1
Fala galerinha bonita, tudo beleza?
Saca só, aqui a gente vai precisar lembrar como é a fórmula para a taxa de passagem de calor em uma parede, dada como:
A chave da questão está ali naquele termo “regime estacionário”. Isso garante que a temperatura em cada ponto fica sempre igual.
Mais importante ainda, isso significa que a taxa da passagem de calor é a mesma em todas as placas.
Passo 2
Então tá, vamos tirar proveito dessa propriedade. Podemos igualar as taxas qualquer par de placas aí. Mas como escolher qual dos pares?
Bom, nós não conhecemos a condutividade da camada , então vamos deixar ela pra lá. A gente também não conhece a temperatura , então não dá pra completar a fórmula da camada .
Vamos igualar as taxas das camadas e então:
A área é a mesma nos dois casos, então podemos cortá-la. Agora é só abrir essas variações de temperatura:
Já temos todos os valores que precisamos, então vamos só isolar o , que é quem queremos achar:
Passo 3
Agora já podemos substituir os valores:
E então:
Resposta
.