Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 11.Exercícios e Problemas - Ex. 40

A FIGURA P11.40 é o gráfico velocidade versus tempo de uma partícula de 500   g que parte de x =   0   m e se move ao longo do eixo x . Desenhe os seguintes gráficos realizando cálculos e plotando pontos correspondentes aos instantes   t =   0 ,   1 ,   2 ,   3   e   4   s . Depois, esboce retas ou curvas com formas apropriadas entre os pontos obtidos. Verifique se incluiu escalas adequadas para ambos os eixos de cada gráfico.

a. Aceleração versus tempo.

b. Posição versus tempo.

c. Energia cinética versus tempo.

d. Força versus tempo.

e. Use seu gráfico de F x versus t para determinar o impulso dado à partícula durante os intervalos 0 - 2   s e 2 - 4   s .

f. Use o teorema impulso-momentum para determinar a velocidade da partícula em t =   2 s e t =   4   s . Seus resultados estão em concordância com o gráfico da velocidade?

g. Agora desenhe o gráfico da força versus posição. Isso não requer qualquer cálculo, apenas reflita cuidadosamente acerca do que obteve nos itens a - d .

h. Use seu gráfico F x versus x para determinar o trabalho realizado sobre a partícula durante os intervalos de tempo 0 - 2   s e 2 - 4   s .

i. Use o teorema trabalho-energia cinética para determinar a velocidade da partícula em t =   2   s e t =   4   s . Seus resultados estão em concordância com o gráfico da velocidade?

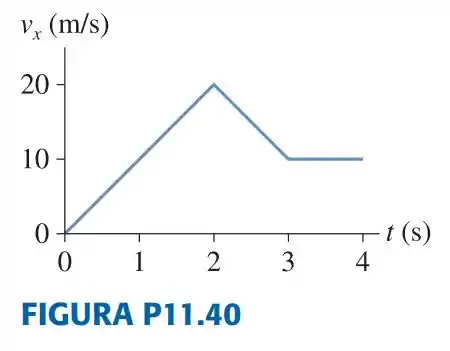
Passo 1

Pessoal se inspirou nessa, bem vamos lá.

Pro gráfico aceleração versus tempo temos que saber que:

a = d v d t = Δ v Δ t

E que a variação de uma reta é constante, portanto no intervalo de tempo entre 0 s   a   2 s teremos:

a = 20 - 0 2 - 0 = 10   m / s 2

Valor esse sendo constante durante todo o intervalo

Agora no intervalo entre 2 s a 3 s temos:

a = 10 - 20 3 - 2 = - 10   m / s 2

E no intervalo entre 3 s a 4   s   temos:

a = 10 - 10 4 - 3 = 0

O que deixa o gráfico da aceleração da seguinte forma

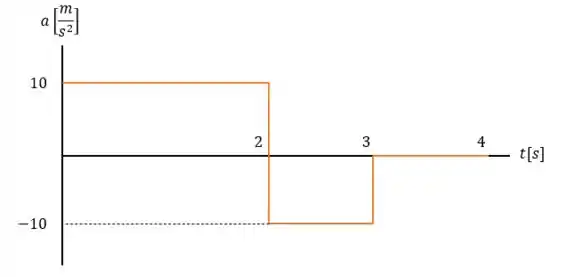
Passo 2

Para fazer o gráfico da posição versus tempo devemos atentar que a posição será:

v = d x d t → x = ∫ v   d t

Portanto no intervalo entre 0 e 2 s a velocidade segue uma função no tempo igual a:

v = 10 t

Então a posição x será igual a:

x = 10 t 2 2 = 5 t 2 + c

Onde que para t = 0 ; x = 0 , pois é dito no enunciado que ele parte de x = 0   m . Portanto para 0 < t < 2 x = 5 t 2 . Onde para t = 2 temos x = 20

----------------------------------Linha simbólica so para dividir um intervalo do outro------------------

Agora no intervalo de 2 < t < 3 temos uma equação de reta igual a:

v = 10 - 20 3 - 2 t + c 1 = - 10 t + c 1

Agora aplicando o ponto ( 2,20 ) temos:

20 = - 10 ⋅ 2 + c 1 → c 1 = 40

Então a equação dessa reta será:

v = - 10 t + 40

Então a equação da posição nesse intervalo de tempo será:

x = - 10 t 2 2 + 40 t + c 2 = - 5 t 2 + 40 t + c 2

Onde sabemos do intervalo anterior que ele começa em t = 2 ; x = 20 portanto c 2 será:

20 = - 5 ⋅ 4 + 40 ⋅ 2 + c 2 → c 2 = - 40

Então no intervalo de 2 < t < 3 ; x = - 5 t 2 + 40 t - 40 , onde para t = 30 temos x = 35   m .

----------------------------------Linha simbólica so para dividir um intervalo do outro------------------

Agora para o intervalo entre 3 < t < 4 temos a reta:

v = 10

Portanto a posição nesse intervalo terá um comportamento de:

x = 10 t + c

Onde temos que para t = 3 ; x = 35 , portanto:

35 = 10 ⋅ 3 + c → c = 5

Então o comportamento da posição no intervalo 3 < t < 4 será x = 10 t + 5

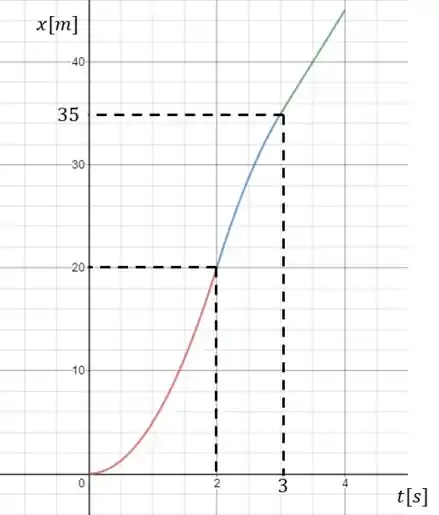
Passo 3

Agora o gráfico energia cinética versus tempo temos que fazer:

K = m v 2 2 = 500 × 10 - 3 2 v 2 = 250 × 10 - 3 v 2

E vamos reescrever aqui todas as funções da velocidade que encontramos no passo anterior:

Portanto a função energia cinética será para cada intervalo:

0 < t < 2 → K = 0.25 × 10 t 2 = 25 t 2

2 < t < 3 → K = 0.25 × - 10 t + 40 2

3 < t < 4 → K = 0.25 × 10 2 = 25   J

Então o gráfico da energia cinética será de:

Passo 4

Agora para o gráfico força versus tempo temos que ter em mente que:

F = m a

E como a massa é de 500 g = 0.5   k g então basta pegarmos o gráfico da aceleração e dividirmos os valores no eixo y por 2.

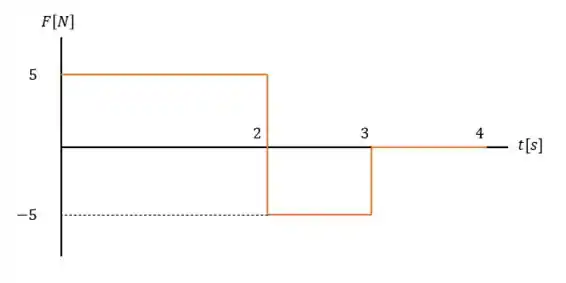
Outra forma de ser ver isso é pelo trabalho, mas né muito trampo.

Passo 5

Agora vamos para a letra e , sabendo que o impulso é:

I = ∫ F d t

Então o impulso em cada intervalo será:

Para 0 < t < 2 :

I = ∫ 0 2 5   d t = 5 t 0 2 = 10   N s

Para 2 < t < 4 , se atente que é até 4 segundos:

I = ∫ 2 3 - 5 d t + ∫ 3 4 0   d t = - 5 t 2 3 = - 5 ⋅ 3 + 5 ⋅ 2 = - 5   N s

Passo 6

Para a f , o momentum (ou momento linear) é encontrado por:

I = Δ p = m ( v f - v 0 )

Então tipo:

v f = v 0 + I m

E como a partícula parte do repouso para 0 < t < 1 então:

v f = 0 + I m = 10 0.5 = 20   m / s

Agora para o intervalo entre 2 < t < 3 temos que v 0 = 20   m / s então:

v f = 20 - 5 0.5 = 10   m / s

E no intervalo entre 3 < t < 4 não temos impulso logo não há variação de velocidade, o que condiz totalmente com o gráfico da velocidade do enunciado.

Passo 7

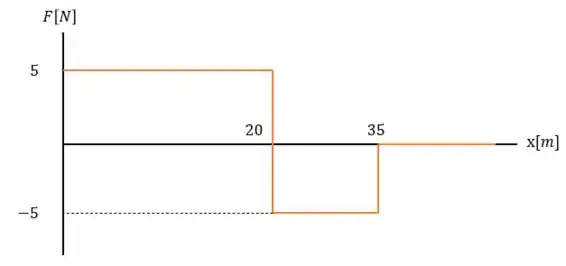
Note que queremos desenhar o gráfico da força versus posição e não força versus tempo na letra g (uau estamos na letra g ).

E como a aceleração é constante e a massa também nos intervalos de 0 < t < 2 ; 2 < t < 3 e 3 < t < 4 então a força também será nesses intervalos o que muda é a posição e isso conseguimos ver no gráfico do Passo 2, o que nos deixa com forças iguais a:

0 < t < 2 ; F = m a = 0.5 × 10 = 5   N

2 < t < 3 ; F = m a = 0.5 × - 10 = - 5   N

3 < t < 4 ; F = m a = 0.5 × 0 = 0   N

Portanto o gráfico será (as posições podem ser vistas no gráfico presente no passo 2).

Passo 8

Letra h

Usando o gráfico do passo anterior temos o trabalho nos intervalos iguais a:

0 < x < 20 → W = 5 × 20 = 100   J

20 < x < 35 → W = - 5 × 35 - 20 = - 75   J

Depois disso o trabalho é nulo.

Passo 9

Finalmente a letra i :

Aqui temos que fazer Δ K = W e para isso vamos fazer por partes:

No intervalo entre 0 < t < 2   s temos que:

m 2 v f 2 - v 0 2 = 100

Onde v o no começo é nulo uma vez que ele parte do repouso, então:

v f = 100 ⋅ 2 0.5 = 20   m / s

E agora para o intervalo entre 3 < t < 4 teremos:

m 2 v f 2 - v 0 2 = - 75

Onde a velocidade inicial é de 20   m / s pois é a velocidade que encontramos no final do intervalo anterior:

Então:

v f = v 0 2 - 75 ⋅ 2 m = 20 2 - 75 ⋅ 2 0.5 = 10   m / s

O que condiz muito com o gráfico da velocidade.

Já no intervalo entra 3 < t < 4 como não temos trabalho nesse intervalo então não há variação da energia cinética, logo não há variação da velocidade. E é isso

F I M

C r é d i t o s   d e   f i l m e   r o l a n d o   s o b r e   a   t e l a

Resposta

a )   I m a g e m   d o   P a s s o   1

b )   I m a g e m   d o   P a s s o   2

c )   I m a g e m   d o   P a s s o   3

d )   I m a g e m   d o   P a s s o   4

e )   P a r a   0 < t < 2 : I = 10   N s

P a r a   2 < t < 4 : I = - 5   N s

f )   E x p l i c a ç ã o   d o   P a s s o   6

g )   I m a g e m   d o   P a s s o   7

h )   0 < x < 20 → W = 100   J

20 < x < 35 → W = - 75   J

i )   E x p l i c a ç ã o   d o   P a s s o   9

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula de 4,00k g está sujeita a uma força resultante que varia com a posição, como mostrado na Figura P6.15. A partícula parte do repouso em x=0 . Qual é a velocidade escalar dela em x=5,00m ,
7 . Na base de um trilho de ar inclinado a um ângulo θ , um planador de massa m é empurrado para deslizar uma distância d para cima na inclinação enquanto diminui sua velocidade e para. Então, o plana
Duas partículas de massas diferentes partem do repouso. A mesma força resultante age sobre ambas quando elas se movem por distâncias iguais. Como se comparam suas energias cinéticas finais? (a) A part
67 . Duas forças constantes agem sobre um corpo de massa m=5,00k g movendo-se no plano x y como mostrado na Figura P6.67. A força F 1 → é 25,0N a 35,0 ° , e a força F 2 → é 42,0N a 150 ° . No momentot