Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 13.Exercícios e Problemas - Ex. 57
Os astrônomos descobriram um sistema estelar binário com período de translação de 90 dias. O sistema consiste de duas estrelas de mesma massa, duas vezes maior que a do Sol, que giram como um haltere em torno do centro de massa, localizado no ponto médio entre elas. Qual é a distância entre as duas estrelas?
Dados:
Massa do sol:
Constante gravitacional universal:
Passo 1
Uma ilustração pode ajudar a gente a entender melhor a situação:
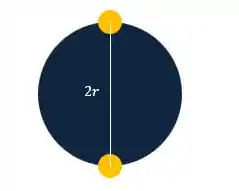
Aqui, é o diâmetro da órbita, e a distância entre as duas estrelas. Podemos considerar isso já que o exercício diz que elas se deslocam na órbita como halteres ao redor do centro da órbita. Assim, fica cada uma em uma extremidade do diâmetro.
Como agora determinar o valor de , pra começar?
Passo 2
Uma estrela vai atuar com força gravitacional sobre a outra. Sendo ambas idênticas, o que fazemos pra uma vale de forma igual pra outra, certo?
Como já visto em exercícios anteriores, a força gravitacional age como força centrípeta (aponta pro centro) e causa o movimento de translação dessas estrelas. O desenho mostra isso com o vetorzinho verde:
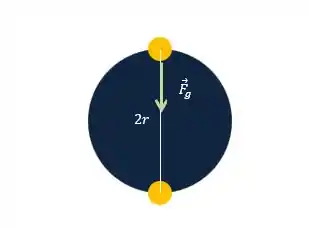
Sendo equivalente à força centrípeta do movimento de translação, podemos escrever:
Onde é a massa de cada uma das estrelas em órbita, e vale a massa do sol.
Igualamos as expressões, simplificamos o que for possível e teremos:
Assim, determinamos uma expressão pra velocidade orbital dessas estrelas. Lembre-se, todo cálculo que estamos fazendo vale pra cada estrela, individualmente, pois são idênticas!
Passo 3
Agora você vai ver que, com essa expressão pra velocidade orbital , conseguimos uma expressão pro período orbital , que já conhecemos o valor.
Lá da cinemática, você sabe que a velocidade de um corpo nada mais é que a distância que ele percorre sobre o tempo , levado pra percorrê-la, certo? Assim:
Pro nosso caso, de uma volta completa pela órbita circular, essa distância equivale ao comprimento da circunferência da órbita: ; o tempo pra isso acontecer vale (período), assim, dias.
Temos assim, a seguinte expressão pra velocidade orbital:
Temos todos os dados que precisamos, e , o valor do raio orbital, vai ser a nossa incógnita. Pra isolá-lo, elevamos ambos os lados ao quadrado pra eliminar a raiz:
Multiplicamos tudo cruzado de forma a isolar e vamos chegar em:
Tiramos a raiz cúbica e teremos:
Passo 4
Agora só aplicamos os valores que já conhecemos e poderemos determinar !
Um pequeno detalhe, antes de seguir, é que o período está dado em dias. Precisamos converter isso pra segundos, pra que tudo fique nas unidades do sistema internacional.
Tendo 1 dia 86400 segundos, 90 dias terão:
Passo 5
Com isso, teremos:
Jogamos tudo isso na calculadora e, no final, vamos ter:
Como queremos a distância entre as estrelas, que vale , o diâmetro da órbita, temos: