Enunciado
Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 6.Problemas - Ex. 67
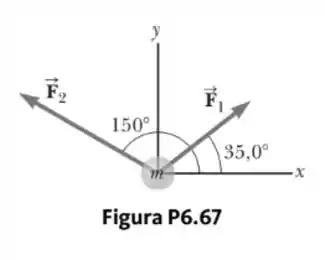
Duas forças constantes agem sobre um corpo de massa movendo-se no plano como mostrado na Figura P6.67. A força é a , e a força é a . No momento, o corpo está na origem e tem velocidade .
- Expresse as duas forças em notação de vetor unitário. Use a notação de vetor unitário para suas outras respostas.
- Encontre a força total exercida sobre o corpo.
- Encontre a aceleração do corpo. Agora, considerando o instante , encontre
- a velocidade do corpo,
- sua posição,
- sua energia cinética a partir de e
- sua energia cinética a partir de .
- Que conclusão você pode tirar, comparando as respostas para as partes (f) e (g)?
Passo 1
Nesse exercício vamos usar equações e conceitos que estamos nos acostumando.
Embora esse exercício tenha muitos itens você não precisa se desesperar pois sei que vai tirar de letra porque vamos fazer passo-a-passo e com bastante detalhe.
Tudo certo? Então bora lá!
Passo 2
Sabemos que:
Então:
Passo 3
A força total exercida pelo corpo é dada por:
Isto é:
Passo 4
Esse item pede a aceleração e podemos encontrá-la facilmente a partir da segunda lei de Newton:
Passo 5
Tendo a aceleração a velocidade também é bem tranquila de encontrar.
Substituindo os valores que já achamos e os valores que o enunciado nos dar:
Passo 6
Vamos usar outra equação da cinemática já muito conhecida por nós:
Passo 7
O enunciado pede a energia cinética a partir de , ou seja:
Passo 8
Agora queremos a energia cinética a partir de de
Passo 9
A energia cinética em e são iguais, isso significa que o teorema de trabalho-energia cinética é consistente com a Segunda Lei de Newton
Resposta
O teorema de trabalho-energia cinética é consistente com a Segunda Lei de Newton