Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Serway e Jewett - Física para cientistas e engenheiros - Vol1 - Ed: 1º - Capítulo 5.Problemas - Ex. 17a

A Figura P4.21 mostra um trabalhador conduzindo um barco – um meio muito eficiente de transporte – em um lago raso. Ele empurra o remo paralelo ao barco, exercendo uma força de módulo 240   N no fundo do lago. Suponha que o remo esteja no plano vertical contendo a quilha do barco. Em um momento, o mastro forma um ângulo de 35,0 ° com a vertical e a água exerce uma força de arrasto horizontal de 47,5   N no barco, oposta à velocidade de avanço de módulo 0,857   m / s . A massa do barco, incluindo sua carga e o trabalhador, é 370   k g .

  1. A água exerce no barco uma força de empuxo verticalmente para cima. Encontre o módulo dessa força.
  2. Considere as forças como constantes durante um curto intervalo de tempo para encontrar a velocidade do barco 0,450   s após o momento descrito.

Passo 1

E aii galera, tudo bem com vocês?

Vamos fazer mais uma questão?

Vem comigo!

Letra a:

Abaixo, um diagrama para melhorar o entendimento:

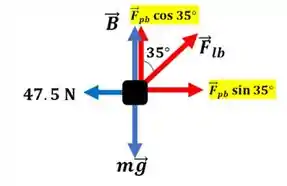
Vamos aplicar a segunda lei de Newton na direção vertical:

∑ F y = m a y

Como a aceleração é zero:

∑ F y = B + F p b s i n ⁡ 35 ∘ - m g = B + 240 cos ⁡ 35 ∘ - ( 370 × 9.8 ) ∴ B = ( 370 × 9.8 ) - 240 c o s ⁡ 35 ∘ = 3.43 × 10 3 N

Passo 2

Letra b:

E agora, vamos aplicar a segunda lei de Newton na direção horizontal:

∑ F x = m a x ∑ F x = F p b sin ⁡ 35 ∘ - 47.5 = 240 sin ⁡ 35 ∘ - 47.5 = 370 a x

a x = 240 sin ⁡ 35 ∘ - 47.5 370 = 0.244 m s 2

Para a velocidade:

v x f = v x i + a x t

v x f = 0.857 + ( 0.244 × 0.45 ) = 0.967   para frente

Resposta

  1. B = 3.43 × 10 3 N
  2. v x f = 0.967  para frente

Exercícios de Livros Relacionados

Após um exame anual, você sai do consultório do seu médico, onde pesava 683N . Depois entra em um elevador que, convenientemente, possui uma balança. Ache o módulo, a direção e o sentido da aceleração
Você é o capitão de uma frota estelar seguindo destemidamente para onde nenhum homem jamais chegou. Você pousa em um planeta muito distante e visita um laboratório de teste de engenharia. Em um experi
Ao saltar a partir de uma posição agachada, uma pessoa normalmente pode atingir uma altura máxima de 60 cm. Durante o salto, o corpo da pessoa dos joelhos para cima normalmente se levanta a uma distân
Uma astronauta está dentro de um foguete com 2,25 × 10 6k g que está subindo verticalmente a partir da plataforma de lançamento. Você deseja que esse foguete alcance a velocidade do som ( 331m / s ) o
Forças durante exercícios de barra fixa. Quando você realiza um exercício de barra fixa, levanta seu queixo pouco acima de uma barra, apoiando-se apenas com seus braços. Normalmente, o corpo abaixo do