Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 4.Problemas - Ex. 55
Você é o capitão de uma frota estelar seguindo destemidamente para onde nenhum homem jamais chegou. Você pousa em um planeta muito distante e visita um laboratório de teste de engenharia. Em um experimento, uma corda leve e curta é afixada ao topo de um bloco e uma força constante de baixo para cima é aplicada à ponta solta da corda. O bloco possui massa e está inicialmente em repouso. À medida que varia, o tempo para o bloco se mover para cima é medido. Os valores que você coletou são dados nesta tabela:
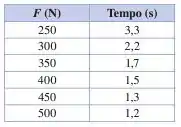
(a) Represente graficamente versus a aceleração do bloco. (b) Use seu gráfico para determinar a massa do bloco e a aceleração da gravidade na superfície do planeta. Observe que, mesmo nesse planeta, os valores medidos contêm algum erro experimental.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente esboçar um gráfico da força versus a aceleração do bloco e usar esse gráfico para determinar a massa do bloco e sua aceleração da gravidade .
Nós sabemos que um bloco é acelerado para cima por uma força de magnitude . Para várias forças, sabemos o tempo para o bloco se mover para cima uma distância de partindo do repouso. Uma vez que a força ascendente é constante, a aceleração também será. E a segunda lei de Newton se aplica ao bloco com essa aceleração.
Como a aceleração é constante, podemos usar a fórmula cinemática:
Onde é a distância vertical percorrida, é a velocidade inicial, o tempo e a aceleração vertical. Além disso, a segunda lei de Newton, , também se aplica ao bloco.
Passo 2
a) Usando a fórmula cinemática vista no passo anterior, com , temos a aceleração:
Nós usamos esta fórmula para calcular a aceleração para cada valor da força na tabela dada. Por exemplo, quando , nós temos:
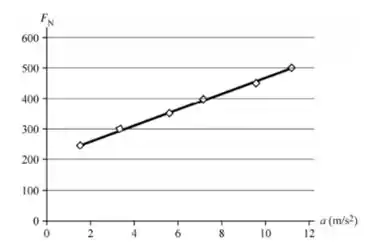
Fazemos cálculos semelhantes para todos os seis valores de e, em seguida, fazemos um gráfico versus . O resultado é mostrado na figura:
Passo 3
b) Agora aplicação da segunda lei de Newton ao bloco, vamos ter:
A equação do nosso gráfico de melhor ajuste na parte (a) é . A inclinação do gráfico é a massa , então a massa do bloco é .
A interceptação é o que dá:
no planeta distante.
Então, a aceleração da gravidade neste planeta não é muito diferente do que é na Terra.
Valeu, galera! Até a próxima! 😉