Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 7.Exercícios e Problemas - Ex. 31
31. A FIGURA P7.31 mostra dois blocos de cada ligados por uma corda. Uma segunda corda está presa ao bloco inferior. As duas cordas têm de massa. O conjunto inteiro é acelerado para cima a pela força .
Quanto vale ?
. Quanto vale a tensão na extremidade superior da corda ?
. Quanto vale a tensão na extremidade inferior da corda ?
. Quanto vale a tensão na extremidade superior da corda ?
Passo 1
Então pessoal, prontos para mais uma?
Se liga no seguinte pessoal, temos que as cordas presentes no sistema tem massa, logo elas vão ter força gravitacional atundo nelas e isso muda muito a situação.
Levando isso em consideração temos os seguintes diagramas de corpo livre.
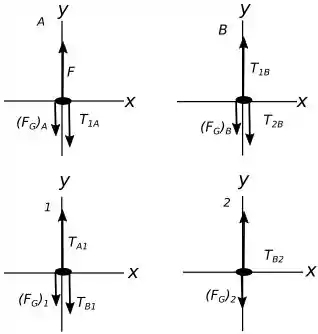
Para encontrar o que é pedido em podemos utilizar a segunda lei de Newton levando em consideração todo o sistema, composto pelos os blocos e pelas cordas, como se fosse uma única massa.
Para encontrar a tensão da parte superior da corda que o item quer vamos fazer a análise do digrama de corpo livre do bloco , utilizando também a segunda lei, já que a parte superior da corda está presa em .
Para os itens e vamos fazer a mesma coisa que para o item só que em relação ao diagrama da corda e em relação ao diagrama do bloco respectivamente.
Vamos lá então galera.
Passo 2
Começando com o item , temos que a segunda lei de Newton para o sistema como se fosse um só fica da seguinte forma:
Substituindo com os valores temos que:
Então temos que:
Passo 3
Agora vamos resolver o item temos que a segunda lei de Newton para o bloco , fica assim:
Isolando que é o que queremos saber, temos:
Substituindo os valores que sabemos, temos:
Passo 4
Agora vamos resolver o item temos que a segunda lei de Newton para a corda , fica assim:
Onde é a tensão que o bloco aplica na corda que é a reação a tensão que a corda aplica em , logo pela terceira lei temos que .
Substituindo tudo que sabemos, temos:
Isolando que é o que queremos, temos:
Passo 5
Agora vamos resolver o item temos que a segunda lei de Newton para o bloco , fica assim:
Onde é a tensão que a corda aplica em que é a reação a tensão que o bloco aplica em , logo pela terceira lei temos que .
Substituindo tudo que sabemos, temos:
Isolando que é o que queremos, temos: