Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Halliday - Vol 4- Ed: 10º - Capítulo 33.7 - Ex. 70

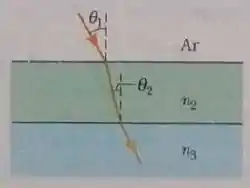
Na figura 33-64, um raio luminoso que estava se propagando no ar incide em um matéria 2 com um índice de refração n 2 = 1,5 . Abaixo do material 2 está o matéria 3, com um índice de refração n 3 . O raio incide na interface ar-material 2 com o ângulo de Brewster para essa interface e incide na interface material 2-material 3 com o ângulo de Brewster para essa interface. Qual o valor de n 3 ?

Passo 1

Sabemos que a lei de Snell nos diz que:

s e n   θ 1   n 1 = s e n   θ 2   n 2

E a lei de Brewster:

θ B = t a n - 1 n 2 n 1

Passo 2

Para encontrarmos o ídice de refração do meio 3 vamos ter que procurar alguma relação entre este meio e os outros dois. Para começar vamos aplicar a lei de Snell duas vezes, do meio 1 para o meio 2 e do meio 2 para o meio 3:

n 2 n 1 n 3 n 2 = tan ⁡ θ B 1 → 2 tan ⁡ θ B 2 → 3

Onde θ B 1 → 2 é o ángulo de Brewster para a superfície entre os meios 1 e 2 e θ B 2 → 3 é o ângulo de Brewster para a superfície entre os meios 2 e 3.

Passo 3

Como as placas são paralelas temos que o ângulo de refração da primeira interface é igual ao ângulo de incidência na segunda interface, mas o ângulo de incidência é o ângulo de Brewster então o ângulo de reflexão será:

θ 2 = θ B 1 = 90 ° - θ 1

Aplicando a tangente desses ângulos temos:

tan ⁡ θ 2 = tan ⁡ θ B 1 = 1 tan ⁡ θ 1

tan ⁡ θ 2   tan ⁡ θ 1 = tan ⁡ θ B 1 = 1

tan ⁡ θ B 1 = n 3 n 1 = 1

Porntanto esse resultado só é possível se n 3 = n 1 = 1

Resposta

O índice de refração n 3 = 1 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um polarizador e um analisador são orientados de modo que se transmita a maior quantidade de luz possível. A que fração da intensidade máxima, o feixe transmitido se reduz quando o analisador gira em
Luz não-palarizada de intensidade 20,0W / c m incide sobre dois filtros polarizadores. O eixo do primeiro filtro forma um ângulo de 25 ° no sentido anti-horário a partir da vertical (vista na direção
Raios de luz com uma intensidade inicial de I 0 passam por dois filtros polarizadores ideais com seus eixos de polarização orientados como mostra a Figura 33.43. Você deseja ajustar o ângulo ϕ de modo
Uma placa de um quarto de onda converte luz linearmente polarizada em luz circularmente polarizada. Prove que uma placa de um quarto de onda também converte luz circularmente polarizada em luz linearm
Um raio de luz solar não-polarizada atinge a parede plástica vertical de um tanque de água em um ângulo desconhecido. Parte da luz se reflete na parede e entra na água (Figura 33.60). O índice de refr