Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 33.Exercícios - Ex. 20
No final da série de óperas de Wagner, O Anel dos Nibelungos. Brunhilda tira o anel de ouro do dedo de Siegfried e joga-o dentro do Reno, onde o anel submerge até o fundo. Supondo que anel fosse pequeno o bastante comparado à profundeza do rio para ser considerado um ponto e que o Reno tenha de profundidade no ponto em que o anel foi jogado, qual é area do maior círculo na superfície da água em que a luz do anel poderia escapar da água?
Passo 1
A luz para de escapar para o ar a partir do momento que atingir o ângulo critico, pois além desse ângulo, ocorrerá apena, a reflexão total da luz. Então vamos descobrir qual é o ângulo critico, e depois vamos achar a área do circulo relacionada a esse ângulo.
Passo 2
Vamos aplicar a lei de snell na interface entre a água e o ar.
Então;
Beleza, então sabemos que para ângulos maiores que esse a luz do anel não escapa para o ar.
Mas como podemos relacionar isso à área de um circulo? Acompanha aqui comigo...
Passo 3
O anel está no fundo do rio de de profundidade. Se aumentarmos mais o ângulo não há refração, então temos que estar a um distância de do ael para que possamos ver a luz refletida por ele. Isso compreende a área de um circulo de raio r.
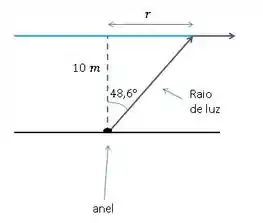
O raio pode ser encontrado a partir de:
Então: