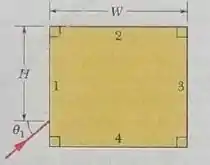
Na figura 33-62, um raio luminoso incide com um ângulo em uma face de um cubo de plástico transparente feito de um material cijo índice de refração é 1,56. As dimensões indicadas na figura são e . A luz atravessa o cubo e chega a uma das faces, onde sofre reflexão (voltada para o interior do cubo) e possivelmente refração (escapando para o ar). Esse é o ponto da primeira reflexão. A luz refletida atravessa novamente o cubo e chega a outra face, onde sofre uma segundra reflexão. Se , determine em que face está (a) o ponto da primeira relexão e (b) o ponto da segunda reflexão. Se existe refração (c) no ponto da primeira reflexão e/ou (d) no ponto da segunda reflexão, determine o ângulo de refração; se não existe, responda “não há refração”. Se , determine em que face está (e) o ponto da primeira relexão e (f) o ponto da segunda reflexão. Se existe refração (f) no ponto da primeira reflexão e/ou (h) no ponto da segunda reflexão, determine o ângulo de refração; se não existe, responda “não há refração”.

a) Aqui precisamos saber em qual face está o ponto da primeira reflexão, para isso vamos fazer uma comparação. Primeiro vamos supor que na refração que ocorre na face 1, a luz consiga chegar no canto inferior direito, se isso acontecer temos que o ângulo da refração pode ser obitido pela tangente pois temos um triângulo retângulo:

Agora podemos ver o que realmente aconteceu levando em conta a lei de Snell. Sabemos que , e o índice de refração do ar é aproximadamente 1, logo:

Portanto como o ângulo de refração do que realmente aconteceu é menor que o ângulo que supomos para o canto superior direito do cubo. Temos que a face onde está localizado o ponto da primeira reflexão é na face 3.

b) Então sabemos que o ponto da primeira reflexão é na face 3 e ele está um pouco abaixo do canto superior direto, mesmo assim continuamos a ter um tirângulo retângulo e partir disso podemos saber o quão abaixo está esse ponto.

O ângulo de refração será 24,33° logo podemos calcular em que local estrá o 2 ponto.

Esse comprimento é menor que , que é o comprimento de , logo temos que o pronto da segunda reflexão será na face 2 do cubo.

c) Para esse caso teremos sim a refração da luz e podemos calcular a partir da lei de Snell. Mas temos que tomar cuidado pois a luz está passando do cunho para o ar, então o ângulo .

d) Já nesse caso nos não teremos um ângulo de refração, pois o ângulo de face 2 medido em relação a normal é:

Que é muito maior que o ângulo crítico para a reflexão interna total. Desta maneira não há refração no ponto da segunda reflexão.

e) Agora pros demais item a ideia é a mesma. Vamos começar comparando os ângulos.

Sabemos que , e o índice de refração do ar é aproximadamente 1, logo:

Portanto como o ângulo de refração do que realmente aconteceu é maior que o ângulo que supomos para o canto superior direito do cubo (37°). Temos que a face onde está localizado o ponto da primeira reflexão é na face 2.

f) Então sabemos que o ponto da primeira reflexão é na face 2 e ele está muito próximo da aresta do canto superior direto, portanto o 2 ponto de reflexão acontecerá na face 2.

g) Nesse caso nos não teremos um ângulo de refração, pois o ângulo de face 2 medido em relação a normal é:

Que é muito maior que o ângulo crítico para a reflexão interna total. Desta maneira não há refração no ponto da primeira reflexão.

h) Já para esse caso teremos sim a refração da luz e podemos calcular a partir da lei de Snell. Mas temos que tomar cuidado pois a luz está passando do cunho para o ar, então o ângulo .