Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 26.7 - Ex. 53

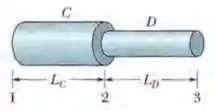
O fio C e o fio D são feitos de materiais diferentes e têm comprimentos L c = L D = 1,0 �� m . A resistividade e o diâmetro do fio C são 2,0 · 10 - 5 Ω · m e 1,00   m m e a resistividade e o diâmetro do fio D são 1,0 · 10 - 6 Ω · m e 0,50   m m . Os fios são unidos da forma mostrada na Fig. 26-34 e submetidos a uma corrente de 2,0   A . Determine a diferença de potencial elétrico (a) entre os pontos 1 e 2 ; (b) entre os pontos 2 e 3 . Determine a potência dissipada (c) entre os pontos 1 e 2 ; (d) entre os pontos 2 e 3 .

Passo 1

Fala aí, pessoal! Tudo certinho? 😉

Aqui temos um fio composto de dois diâmetros e resistividades diferentes, e é submetido a uma corrente. Temos que calcular a diferença de potencial entre os pontos 1 e 2 , 2 e 3 . A potência dissipada entre 1 e 2 , 2 e 3 .

Tem ideia de como fazemos isso? 👀

Primeiro precisamos determinar a resistência equivalente de cada fio pela equação

R = ρ L A

E pela lei de Ohm, determinar a tensão

V = R i

Com a tensão V , corrente i e a resistência R , podemos determinar tambem a potência

P = V i = V 2 R = R i 2

Sacou? Bora começar! 😬

Passo 2

(a)Para saber a diferença de potencial entre os pontos 1 e 2 usamos a Eq. 26-16,

R = ρ L A → R C = ρ C L C π r C 2

Se ρ = 2,0 × 10 - 6 Ω . m , L C = 1,0 m e r C = 5 × 10 - 4 , então

R C = 2,0 × 10 - 6 Ω . m 1,0 m π 5 × 10 - 4 2

R C = 2,55 Ω

e, de acordo com a Eq. 26-8, se i = 2,0 A

V 1 - V 2 = V C = i R C = 2,0 A × 2,55 Ω

V 12 = 5,1 V

Bacana, não é? 😐

Passo 3

(b) Da mesma forma que o item anterior

R D = ρ D L D π r D 2

Se ρ D = 1,0 × 10 - 6 Ω . m , L D = 1,0 m e r D = 2,5 × 10 - 4 , então

R D = 1,0 × 10 - 6 Ω . m 1,0 m π 2,5 × 10 - 4 2

R D = 5,09 Ω

Como i = 2,0 A

V 2 - V 3 = V D = i R D = 2,0 A × 5,09 Ω

V 23 = 10,2 V

Está acompanhando? 😬

Passo 4

(c) De acordo com a Eq. 26-27,

P C = i 2 R C = 10 W

(d) Analogamente,

P D = i 2 R D = 20 W .

E aí, entendeu tudo? Responde Aí! 😉

Resposta

(a) V 1 - V 2 = 5,1 V

(b) V 2 - V 3 = 10 V

(c) P C = 10 W

(d) P D = 20 W .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma máquina de cachorro-quente funciona aplicando uma diferença de potencial de 120 V às extremidades de uma salsicha e cozinhando-a com a energia térmica produzida. A corrente é 10,0 A e a energia ne
Na Fig. 26-3 la, um resistor de 20 Ω é ligado a uma bateria. A Fig. 26-3 lb mostra a energia térmica E, gerada pelo resistor em função do tempo t . A escala vertical é definida por E t , S , = 2,50 m
Na Fig. 26-32, uma bateria com uma diferença de potencial V = 12 V está ligada a um fio resistivo de resistência R = 6,0 Ω . Quando um elétron percorre o fio de um extremo a outro, (a) em que sentido
Um fio de cobre com uma seção reta de 2,00 × 10 - 6 m 2 e um comprimento de 4,00 m é percorrido por uma corrente uniformemente distribuída. (a) Qual é o módulo do campo elétrico no interior do fio ? (
Uma lâmpada de 100 W é ligada a uma tomada de parede de 120 V. (a) Quanto custa deixar a lâmpada ligada continuamente durante um mês de 31 dias? Suponha que o preço da energia elétrica é $0,06/kW · h.