Como as fórmulas para a lei da gravidade de Newton e para a lei de Coulomb têm a mesma dependência com o inverso do quadrado da distância, uma fórmula análoga à da lei da Gauss pode ser determinada para a gravidade. O campo gravitacional em uma determinada posição é a força por unidade de massa em uma massa de teste colocada naquela posição. (Então, para uma massa puntiforme na origem, o campo gravitacional na posição é . Determine o fluxo do campo gravitacional através de uma superfície esférica de raio centrada na origem e verifique que o análogo gravitacional para a lei de Gauss é
Passo 1
Fala aí, beleza? Então, a gente quer fazer um paralelo entre a lei de Gauss para a eletricidade e a Lei de Gauss para a gravitação... podemos fazer isso pois tanto a Lei de Coulomb e a Lei da Gravitação Universal possuem a mesma cara. Veja:
Vamos fazer uma conjectura de como vai ficar a lei de Gauss. Notemos que temos os seguintes termos correlacionados:
Como a Lei de Gauss para a eletricidade é:
então, esperamos para a gravidade:
Agora vamos provar isso calculando o fluxo do vetor em uma esfera centrada na origem.
Passo 2
Temos que
Assim, queremos calcular
essa integral será calculada na superfície de uma esfera que possui a massa localizada em seu centro (veja a figura abaixo).
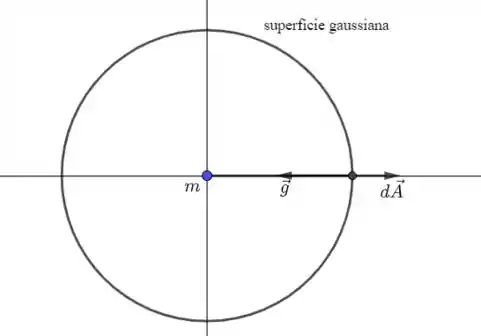
Notemos que é constante sobre cada ponto da esfera. Além disso,
Assim,
Porém, essa última integral é simplesmente a área da esfera:
Dessa maneira, segue que:
que é exatamente o mesmo resultado obtido anteriormente!
Resposta
O fluxo é .