Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Moysés - Vol. 3- Ed: 1º - Capítulo 3.Problemas - Ex. 8

O valor médio do campo elétrico na atmosfera num determinado dia, num ponto da superficície da Terra é de 300 N / C , dirigido verticalmente para baixo. A uma altitude de 1400   m , ele reduz-se a 20   N / C . Qual a densidade média de carga na atmosfera abaixo de 140 0   m ?

Passo 1

Se liga! Podemos desenhar as informações que ele nos deu no enunciado da seguinte forma

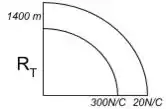
Podemos escrever o campo para superfície da terra como

E S = k q 1 R T 2 ⟹ q 1 = E s R T 2 k

Para facilitar as nossas continhas, diremos que

r = 1400   m   .

Sendo assim, na altitude citada o campo será

E A =   k q 2 R T + r 2   ⇒ q 2 = E A R T + r 2 k

Passo 2

Portanto a diferença entre a as cargas é

Δ q =   E s R T 2 k - E A R T + r 2 k   .

Passo 3

Como queremos estamos interessados na densidade média, precisamos saber

ρ = Δ q Δ V

O diferença de volume é

Δ V = 4 3 π R T + r 3 - R T 3 =   4 3 π r 3 R T 2 + 3 R T r + r 2

Passo 4

Agora só precisamos fazer a razão

ρ = 1 k E S R T 2 - E A R T + r 2 4 3 π r 3 R T 2 + 3 R T r + r 2

Usando os valores dados no eneunciado

E S = 300   N / C

E A = 20   N / C

Considerando o raio da Terra

R T ≈ 6731   k m

Agora só precisamos substituir os valores na expressão do ρ , fazer essa conta e correr para o abraço!

ρ ≈ 1,8 × 10 - 12   C / m 3

Resposta

ρ ≈ 1,8 × 10 - 12   C / m 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No modelo clássico de J.J. Thomson para átomo de hidrogênio, a carga + e do núcleo era imaginada como sendo uniformemente distribuída no interior de uma esfera de raio a da ordem de 10 - 8c m (raio at
Uma casca esférica de raio interno b e raio externo c, uniformemente carregada com densidade de carga volumétrica ρ , envolve uma esfera de raio a , também carregada uniformemente com a mesma densidad
Uma distribuição de carga esférica simétrica tem densidade volumétrica de carga dada por ρ r = ρ 0 exp ⁡ - r a ( 0 ≤ r∞) onde ρ 0 é uma constante e r é a distância à origem. Calcule a carga total da d
Uma casca esférica de raio interno b e raio externo c, uniformemente carregada com densidade de carga volumétrica ρ , envolve uma esfera de raio a , também carregada uniformemente com a mesma densidad
Uma casca esférica de raio interno b e raio externo c, uniformemente carregada com densidade de carga volumétrica ρ , envolve uma esfera de raio a , também carregada uniformemente com a mesma densidad