Um gás é submetido a uma expansão isotérmica reversível num recipiente cilídrico munido de um pistão de área e massa . O pistão desloca-se na direção com velocidade constante . Tem-se e , onde é a velocidade quadrática média das moléculas, cuja massa é . Suponha as colisões das moléculas com o pistão perfeitamente elásticas num referencial que se move com o pistão. (a) Mostre que, no referencial do laboratório (onde o cilindro está em repouso), as colisões com o pistão não são perfeitamente elásticas, calculando a perda de energia cinética de uma molécula que colide com o pistão com componente da velocidade (no resultado, despreze em confronto com ). (b) Some sobre todas as moléculas e mostre que a perda total de energia cinética é igual ao trabalho realizado na expansão do gás.
Passo 1
(a) Nossa primeira tarefa é calcular a variação de energia cinética da molécula que colide com o pistão.
No referencial do pistão, a velocidade com que a molécula chega deve ter o mesmo módulo da velocidade com que ele sai, mas sentidos opostos.
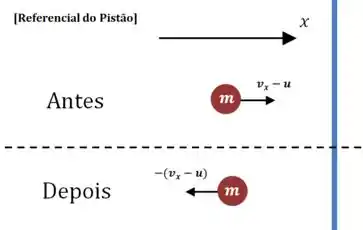
Nesse desenho, é a velocidade do pistão, que pode ter sinal positivo ou negativo, dependendo do sentido.
Agora queremos passar isso para o referencial do laboratório. Para isso só precisamos somar a todas as velocidades que escrevemos.
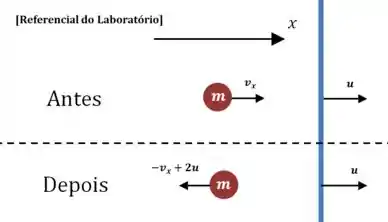
E note que aquele vetor que indica a velocidade do pistão pode ter um sentido diferente, dependendo do sinal de .
Passo 2
Beleza, agora é só calcular a diferença de energia cinética entre o antes e depois no referencial do laboratório;
Vamos colocar em evidência:
E conforme a sugestão do enunciado, vamos ignorar os termos em que aparece elevado ao quadrado:
Pronto! Mostramos que a colisão não é perfeitamente elástica, porque a molécula perde alguma energia cinética.
Se tivermos moléculas, a perda total de energia cinética será:
Passo 3
(b) Ok, agora o próximo passo é calcular o trabalho realizado pelo gás, e mostrar que é igual à variação de energia cinética que acabamos de calcular.
Vamos começar pela definição de trabalho:
Onde é a força realizada e é o deslocamento do pistão. Agora vamos reescrever a força a partir da variação de momento:
Usando a mesma imagem de antes, dá pra ver que a variação de momento de cada molécula é:
E temos que colocar um para considerar a contribuição de todas as moléculas:
Passo 4
Agora vamos substituir na expressão que encontramos para o trabalho:
E podemos reescrever com , que é simplesmente a velocidade do pistão no referencial do laboratório:
E finalmente, vamos usar a mesma aproximação de antes:
Então:
E chegamos no resultado esperado: o trabalho é igual à variação da energia cinética!
Resposta
(a) A perda de energia cinética é .
(b) O trabalho realizado na expansão do gás é .