Trace as figuras de Lissajous corerespondentes à composição dos seguintes movimentos harmônicos simples em direções perpendiculares:
(a) , .
(b) , .
Sugestão: Use o método dos dois círculos de referência.
Passo 1
(a) Vamos tentar usar o método dos dois círculos de referência.
Nessa primeira figura, a coordenada vai ser tirada dessa função aqui:
Mas pensando bem, isso é simplesmente a componente horizontal de um vetor de magnitude e que roda com frequência angular :
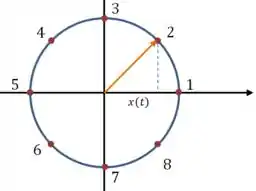
E a coordenada vai ser tirada de outra função:
Que é a componente vertical de um vetor que gira com o dobro da velocidade do de cima. A gente pode representar essa diferença de velocidade pela numeração dos pontos:
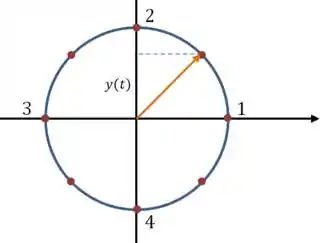
Até aqui fizemos tudo como se . Isso não afeta o formato das figuras, só a escala.
Passo 2
Agora é só juntar esses dois conjuntos de pontos! Colocando na vertical e na horizontal, juntando os pontos com números iguais:
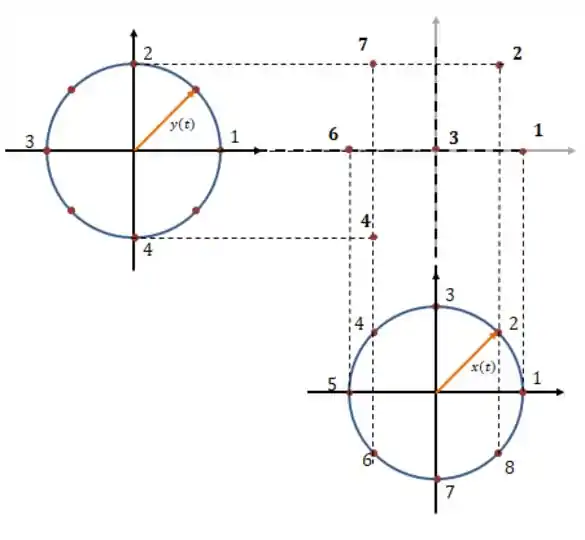
Agora é só continuar completando esses pontos! Sabendo que devemos esperar algum tipo de curva. O resultado vai ser o seguinte:
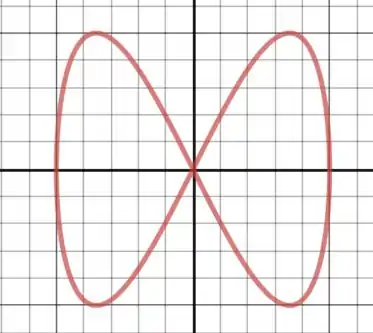
Passo 3
(b) Agora vamos fazer a mesma coisa com essas coordenadas aqui:
O que isso quer dizer? Temos os mesmos vetores de antes, mas agora vamos pegar a componente vertical do primeiro, e a componente horizontal do segundo.
Esse caso é um pouco mais difícil de desenhar. Pelo primeiro gráfico, a gente vai tirar alguns “comprimentos” que vão dar as coordenadas horizontais:
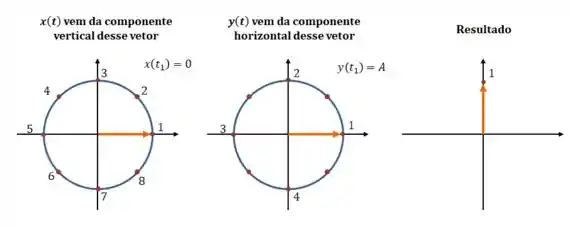
Vamos continuar por mais alguns pontos:
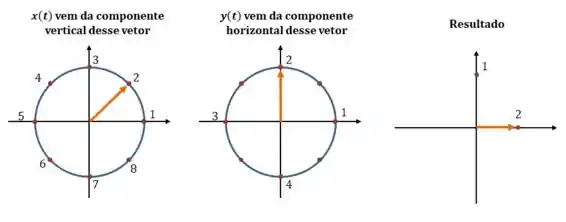
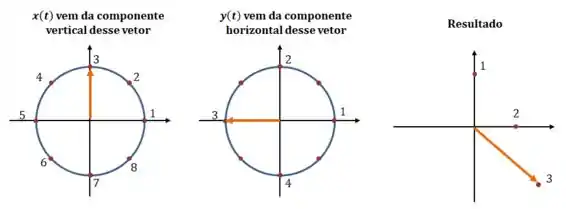
Continuando esse ciclo, você vai chegar num desenho como esse aqui:
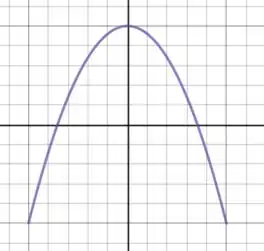
Resposta
Ver desenhos.