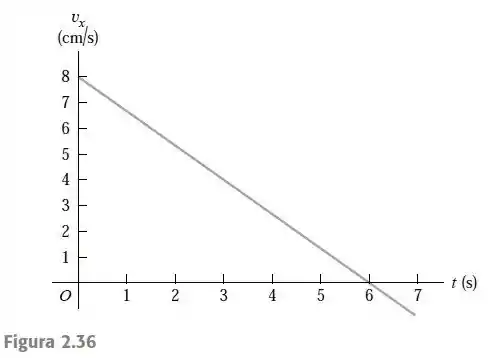
Um gato anda em uma linha reta, à qual chamaremos de eixo com a direção positiva para a direita. Como um físico observador, você mede o movimento desse gato e desenha um gráfico da velocidade do felino em função do tempo (Figura 2.36).
a) Determine a velocidade do gato a e a .
b) Qual é a aceleração do gato a ? A ? A ?
c) Qual é a distância percorrida pelo gato nos primeiros 4,5 s? De t = 0 até t = 7,5 s?
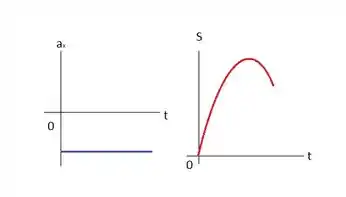
d) Desenhe gráficos claros da aceleração e da posição do gato em função do tempo, supondo que ele partiu da origem.
Passo 1
Bom, aqui podemos relacionar a posição que o gato se encontra com o tempo, usando:
Do gráfico, observamos que:
e
Também, que:
.
Passo 2
Mas, primeiro, precisamos descobrir a aceleração, .
Observe que temos todas as componentes para substituir na seguinte equação:
E isolarmos a aceleração, :
Pronto!
Já podemos substituir os valores na primeira formula:
Vamos guardar essas informações.
Passo 3
- Queremos saber a velocidade do gato no instante .
- Como calculamos lpa em cima, a aceleração do gato é contante, e diferente de zero, durante todo o percurso.
- Então pessoal , para acharmos a distância percorrida temos que achar a posição do gato em tempos estratégicos. Neste caso , temos que:
- Calculamos a aceleração, no caso, negativa, e esta foi utilizada para todos os itens do exercício, logo ela é constante, representada pela reta em azul, mas como a velocidade varia ao longo do tempo, obtemos uma curvatura, em vermelho.
Como agora temos a aceleração, , podemos substituir os valores na equação da velocidade em um instante de tempo:
Agora vamos seguir o mesmo raciocínio para o instante :
Passo 4
Isso nos diz que temos um movimento retilíneo uniformemente variado.
Passo 5
Para (início das duas situações) :
Para (final da primeira situação):
Agora vou
Para (momento que o gato passa a andar no sentido contrário) :
Para (final da segunda situação):
Agora fica mais tranquilo, só precisamos lembrar que a distância percorrida é a soma dos módulos dos deslocamentos em todos os sentidos.
Para a primeira situação , o gato anda em um único sentido , logo:
Já para a segunda situação o gato anda em dois sentidos , então temos que dividir o problema no ponto exato da mudança de movimento:
Passo 6
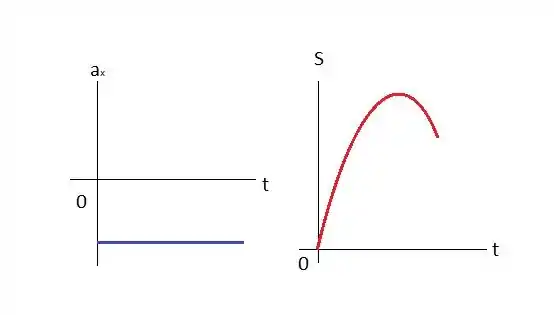
Resposta
- Para e para ;
- e