Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.Problemas - Ex. 74

Uma velejadora encontra ventos que impelem seu pequeno barco a vela. Ela veleja 2,0 km de oeste para leste, a seguir 3,50 km para sudeste e depois, a certa distância em direção desconhecida. No final do trajeto ela está a 5,80 km diretamente a leste de seu ponto de partida (Figura 1.39). Determine o módulo e a direção do terceiro deslocamento. Faça um diagrama em escala da soma vetorial dos deslocamentos e mostre que ele concorda aproximadamente com o resultado obtido mediante a solução numérica.

Passo 1

E aí, galerinha!

Se no final a velejadora está em R → de valor 5,80Km no eixo x, isso significa que R → é a soma de todas as trajetórias. Então a gente só precisa somar as componentes das trajetórias e igualar às componentes de R → pra achar as componentes de C → . Depois é só usar Pitágoras pra achar o módulo e usar a tangente para encontrar o ângulo dessa trajetória.

Só bora!

Passo 2

Vamos começar decompondo as trajetórias em x e em y. Começando por x:

A x + B x + C x = R x

C x = R x - B x - A x

C x = 5,8 - 3,5 c o s 45 ° - 2

C x = 1,33 k m

Agora em y:

C y = R y + B y - A y

C y = 0 + 3,5 s e n 45 ° - 0

C y = 2,47 k m

Tranquilo até aqui?

Passo 3

Agora que temos as componentes, usamos Pitágoras pra encontrar o módulo da trajetória C → .

C =   C x 2 + C y 2

C = 1,33 k m 2 + 2,47 k m 2

C = 2,81 k m

Uhuu! Achamos o módulo, agora bora pro ângulo.

Passo 4

Como as componentes são positivas, a trajetória C → faz ângulo com o eixo +Ox.

Pra saber esse ângulo, vamos usar a tangente:

t g α = C y C x = 2,47 k m 1,33 k m = 1,86

Agora usamos o arco-tangente pra descobrir esse ângulo maravilhoso:

a r c t g 1,86 = 61,7 °

Estamos quase lá!

Passo 5

Agora vamos desenhar o diagrama:

Para obter o diagrama do vetor R resultante colocamos um vetor seguido do outro, ou seja, o inicio de um vetor no final de outro vetor...

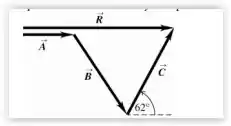
E ele concorda plenamente com os dados obtidos.

Conseguimos! Entendeu tudo? Responde Aí! 😉

Resposta

Módulo: 2,81km

Direção: 61,7° com o eixo +Ox

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o vetor unitário (em termos de i ^ e j ^ ) com a orientação oposta à orientação de cada um dos vetores A → ,B → e C → do Problema 57.
São dados os seguintes vetores: A → vale 25l b e forma um ângulo de 30 ° no sentido horário com o eixo + x e B → vale 42l b e forma um ângulo de 50 ° no sentido horário com o eixo + y . (a) Faça um es
Reescreva os seguintes vetores em termos da magnitude e do ângulo (medido no sentido anti-horário a partir do eixo + x ). (a) Um vetor deslocamento com uma componente x de + 8,5m e uma componente y de
Usando o produto vetorial, prove a lei dos senos para o triângulo mostrado na figura 10-43. Isto é, se A ,B e C são comprimentos de cada lado do triângulo, mostre que A s e n a = B s e n b = C s e n c
Para os vetores A→ e B → incicados na Fígura 1.34 use diagramas em escala para determinar a) a soma vetorial A → + B → b) a diferença vetorial A → – B → . Use suas respostas para encontrar o módulo e