Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 2.Problemas - Ex. 88

Uma estudante está se deslocando com sua velocidade máxima de 5,0 m/s para pegar um ônibus parado no ponto. Quando ela está a uma distância de 40,0 m do ônibus, ele começa a se mover com aceleração constante igual a 0,170 m/s2 . (a) Durante quanto tempo e por qual distância a estudante deve correr a 5,0 m/s para que alcance o ônibus? (b) Quando a estudante alcança o ônibus, qual é a velocidade dele? (c) Faça um gráfico de xt para a estudante e para o ônibus. Considere x 0 como a posição inicial da estudante. (d) As equações usadas para calcular o tempo na parte (a) possuem uma segunda solução, que corresponde a um tempo posterior para o qual a estudante e o ônibus estão na mesma posição, caso continuem com seus movimentos especificados. Explique o significado dessa segunda solução. Qual é a velocidade do ônibus neste ponto? (e) Caso sua velocidade máxima fosse igual a 3,5 m/s, ela poderia alcançar o ônibus? (f) Qual seria a velocidade mínima para que ela pudesse alcançar o ônibus? Neste caso, quanto tempo e qual seria a distância percorrida para que a estudante pudesse alcançar o ônibus?

Passo 1

Letra a:

Considere que a origem está na posição inicial do aluno e a direção x positiva é a direção em que o ônibus está se movendo. A aluna está inicialmente em x s 0 = 0 m e o ônibus x b 0 = 40 m .

Para x s = x b

x s = v s t x b = x b 0 + v b 0 t + 1 2 a b t 2

Fazendo as equações, temos o seguinte:

v s t = x b 0 + v b 0 t + 1 2 a b t 2 v s t = x b 0 + 1 2 a b t 2 1 2 a b t 2 - v s t + x b 0 = 0

Agora temos a equação quadrática com a = 1 2 a b , b = - v s   e   c = x b 0 :

t = - b ± b 2 - 4 a c 2 a

t = v s ± v s 2 - 2 a b x b 0 a b t = 5 ± 5 2 - 2 × 0.17 × 40 0.17 t = 9.55 s   e   t = 49.27 s

A aluna pega o ônibus depois de t = 9.55 s , mas se ela decidisse não ir de ônibus e continuar a correr ela iria passar o ônibus. Depois de t = 49.27 s de quando ela começou a correr o ônibus iria alcançá-la novamente.

A distância que a aluna corre nesses 9.55 s é

d = v s t = 5 × 9.55 = 47.75 m

Passo 2

Letra b:

Use a equação cinemática:

v b = v b 0 + a b t v b = 0 + 0.17 × 9.55 = 1.62 m s

Passo 3

Letra c:

Tome a origem na posição inicial do aluno assim, x s 0 = 0   e  x b 0 = 40 m .

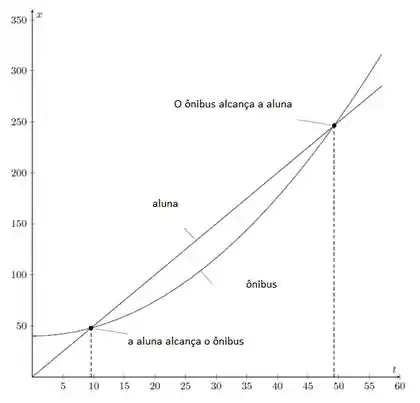
Passo 4

Letra d:

A segunda solução representa o caso em que se a aluna decidiu não pegar o ônibus e continue a correr. Ela iria passar o ônibus. Depois de t = 49.27 s desde quando ela começou a correr o ônibus a alcançaria novamente.

Neste ponto, o ônibus estaria viajando em:

v b = v b 0 + a t v b = 0 + 0.17 × 49.27 = 8.38 m s

Passo 5

Letra e:

Igual a letra a, mas dessa vez temos a = 1 2 a b ,     b = - v s = 3.5 m / s   e   c = x b 0 = 40 m :

t = v s ± v s 2 - 2 a b x b 0 a b

Agora a parte sob a raiz tem valor negativo porque v s 2 < 2 a b x b 0   dá uma solução imaginária para a aluna que não seria capaz de pegar o ônibus.

Passo 6

Letra f:

A partir da equação quadrática obtivemos na letra a, para o aluno alcançar o ônibus a parte raiz da fórmula tem que ser real. Isso requer que v s 2 > 2 a b x b 0 . Então:

v s m i n = 2 a b x b 0 = 2 × 0.17 × 40 = 3.688 m s

Para calcular o tempo, vamos novamente para a equação quadrática e substitua por v s = 3.688 m / s :

t = v s ± v s 2 - 2 a b x b 0 a b t = 3.688 ± 3.688 2 - 2 × 0.17 × 40 0.17 t = 21.91 s

A distância que o aluno se move:

d = v s t = 3.688 × 21.7 = 80 m

Resposta

  1. t = 9.55 s , d = 47.75 m
  2. v b = 1.62 m s
  3. v b = 8.83 m s
  4. Não, ela não pode pegar o ônibus
  5. v s m i n = 3.688 m / d , t = 21.7 s , d = 80 m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce uma representação pictórica para o seguinte problema. Não o resolva de fato. O semáforo torna-se verde, e uma ciclista parte com aceleração de 1,5m / s 2 . Quanto ela terá percorrido até atingi
Em uma gincana, cada concorrente corre 25,0m transportando um ovo equilibrado em uma colher, dá a volta e retorna ao ponto de partida. Edite corre os primeiros 25,0m em 20,0s . Quando volta, ela se se
De acordo com um artigo da revista Scientific American (maio de 1990), circulam normalmenteem uma auto-estrada americana cerca de 2400 veículos por hora em cada pista, com velocidade de96k m / h para
Em uma competição de bicicletas com percurso de 30k m , você percorre os primeiros 15k m com uma velocidade média de 12k m / h . Qual deve ser sua velocidade escalar média nos 15k m restantes para que
Daniel dirige na Estrada I-80 em Seward, no Estado de Nebraska, e segue por um trecho retilíneo de leste para oeste com uma velocidade média com módulo igual a 88k m / h . Depois de percorrer 76k m ,