Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.Problemas - Ex. 78
O retorno. Um explorador de uma densa floresta na África equatorial deixa sua cabana. Ele dá 40 passos no sentido nordeste, depois 80 passos em uma direção que forma um ângulo de 60° considerando a rotação no sentido do oeste para o norte, a seguir 50 passos diretamente para o sul. Considerando-se que os seus passos têm o mesmo comprimento a) Faça um diagrama aproximadamente em escala dos três vetores e da resultante da soma vetorial. b) Ajude-o a evitar se perder na floresta fornecendo-lhe o vetor deslocamento, calculado pelo método dos componentes, necessário para que ele retorne para sua cabana.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos diz que um explorador deixa sua cabana e faz o seguinte caminho:
- Ele dá passos no sentido nordeste;
- Depois ele dá passos em uma direção que forma um ângulo de considerando a rotação no sentido do oeste para o norte;
- A seguir ele dá passos diretamente para o sul.
Queremos transformar essas informações em vetores e, com isso, encontrar o vetor resultante.
Bom... com os dados do enunciado você vai imaginar os caminhos que o explorador faz e pra fazer a soma vetorial é só ligar uma linha reta entre o início do trajeto e o final dele.
Passo 2
Seja o vetor os passos no sentido nordeste, o vetor os passos com a rotação de em relação ao norte e o vetor os passos em direção ao sul.
E seja o vetor a resultante dos três vetores.
O diagrama vai ficar mais ou menos assim:
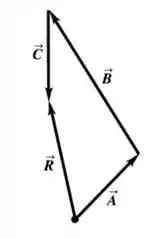
Agora partiu letra b)!
Passo 3
A letra b) quer saber o vetor deslocamento pra que o explorador volte pra casa, e sem se perder. HEHE.
Como ele vai voltar pra casa, o trajeto dele vai fechar e isso significa que a soma vetorial de todos os trajetos vai ser .
Agora tudo ficou mais fácil! Pra achar o módulo é só decompor as trajetórias em e em fazendo a soma dar . Assim a gente vai encontrar as componentes do vetor deslocamento. Depois é só usar o nosso querido Pitágoras 😉.
A direção pode ser dada através do ângulo com o eixo x e vamos acha-lo através da tangente. Então bora lá!
Passo 4
Vamos decompor os trajetos em :
Agora em :
Passo 5
Agora que temos as componentes, vamos usar o maravilhoso Teorema de Pitágoras pra achar o módulo do deslocamento:
Então sabemos que para o explorador voltar pra casa ele vai ter que dar 49 passos. Mas em qual direção?
Vamos ver:
Passo 6
Pra achar o ângulo que o vetor deslocamento faz com o eixo x, vamos primeiro usar a tangente desse ângulo:
Agora usamos o arco-tangente pra encontrar o ângulo:
Então ele vai ter que andar 49 passos a 76° graus considerando a rotação do leste pro sul.
“Its finished!” \O/
Resposta
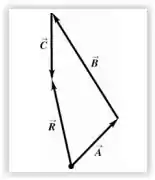
- Módulo: 49 passos; Direção: 76° no sentido da rotação do leste pro sul.