Um ímã em barra está montado na extremidade de uma mola e oscila em movimento harmônico simples ao longo do eixo de um anel, como mostrado na Figura 28-40. O ímã está em sua posição de equilíbrio quando seu ponto médio está no plano do anel.
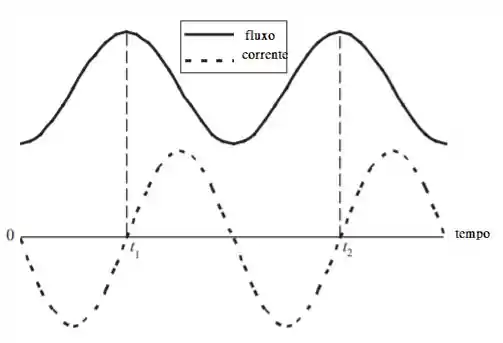
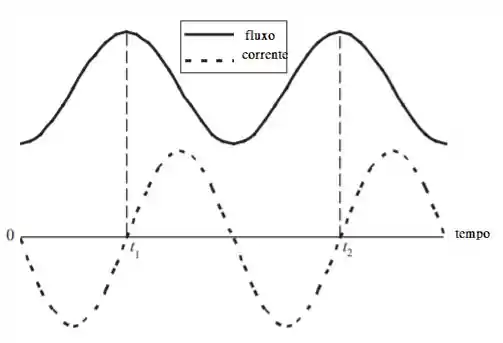
- Faça um gráfico do fluxo magnético através do anel como função do tempo. Indique quando o ímã estiver à metade do caminho no anel, identificando estes instantes por e
- Faça um gráfico da corrente induzida no anel como fungao do tempo, escolhendo o sentido positivo da corrente como sendo o horário quando visto de cima.

Passo 1
Como o ímã se move com um simples movimento harmônico, o fluxo e a corrente induzida irão variar de modo senoidal. A corrente será um máximo onde o fluxo está mudando mais rapidamente e será zero onde o fluxo é momentaneamente constante.
Passo 2
Letra a e b:
O gráfico a seguir mostra o fluxo, , e a corrente induzida (proporcional a no anel em função do tempo.
Resposta