Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 29.Problemas - Ex. 56

Uma barra condutora com comprimento L = 0.8 m está livre para deslizar sem atrito sobre trilhos horizontais, como indica a figura 29.48. Há um campo magnético uniforme B = 1.5 T , orientado para dentro do plano da figura. Em uma das extremidades dos trilhos há uma bateria com fem ε = 12 V e uma chave. A barra possui massa de 0.9 k g e resistência de 5.0   Ω , e todas as demais resistências no circuito podem ser ignoradas. A chave é fechada no instante t = 0 .

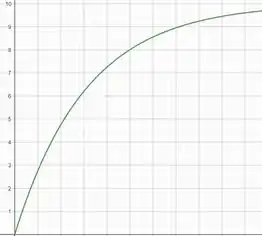
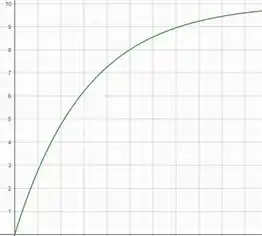
a Faça um desenho da velocidade escalar da barra em função do tempo.

b Logo após a chave ser fechada, qual é a aceleração da barra?

c Qual é a aceleração da barra quando sua velocidade escalar é igual a 2,0   m / s ?

d Qual é a velocidade terminal da barra?

Passo 1

Para resolvermos essa questão vamos aplicar a segunda lei de Newton. Nossa barra experimentará força magnética devido a corrente induzida no loop ao movimentá-la. Vamos utilizar ainda que a = d v / d t e resolveremos a equação para v , lembrando que na velocidade terminal temos a = 0 . Pois bem, outra consideração que devemos levar em conta para a resolução do problema é que a magnitude da força eletromotriz induzida terá magnitude B L v e será dada no sentido anti-horário, por isso se opõe à voltagem da bateria ε .

Passo 2

A corrente líquida no nosso loop será dada por

I = ε - B L v R

Já a aceleração da barra será

a = F m = I L B ⋅ sin ⁡ 90 ° m → a = ε - B L v ⋅ L B m

Utilizando o fato que a = d v d t podemos encontrar uma expressão para v t usando o método de separação de variáveis. Assim, teremos

d v d t = ε - B L v ⋅ L B m → d v ε - B L v = L B m R   d t

Integrando ambos os lados vamos encontrar

∫ 0 v d v ε - B L v = ∫ 0 t L B m R   d t → v t = ε B L ⋅ 1 - e - B 2 L 2 t m R = 10 ⋅ 1 - e - t 3.1

Esse gráfico pode ser representado por

Passo 3

Apenas depois da chave ser fechada teremos

v = 0 ,     I = ε R = 2.4 A

F = I L B = 2.88 N ,     a = F m = 3.2   m / s 2

Passo 4

Quando v = 2.0   m / s teremos

a = 12 - 1.5 ⋅ 0.8 ⋅ 2.0 ⋅ 0.8 ⋅ 1.5 0.9 ⋅ ( 5.0 ) = 2.6   m / s 2

Por fim, devemos notar que à medida que a velocidade aumenta, a aceleração diminui. A velocidade se aproxima assintoticamente da velocidade do terminal

ε B L = 12 1.5 ⋅ 0.8 = 10   m / s

Fazendo com que a aceleração seja igual a 0.

Resposta

a

b   a = 3.2   m / s 2

c   a = 2.6   m / s 2

d  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um solenoide longo tem um diâmetro de 12,0c m . Quando o solenoide é percorrido por uma corrente i , um campo magnético uniforme de módulo B = 30,0m T é produzido no interior. Através de uma diminuiçã
A Fig. 30-54 mostra duas regiões circulares, R 1 e R 2 , de raios r 1 = 20,0c m e r 2 = 30,0c m . Em R 1 existe um campo magnético uniforme de módulo B 1 = 50,0m T dirigido para dentro do papel e em R
O campo magnético de um ímã cilíndrico com 3,3c m de diâmetro varia senoidalmente entre 29,6T e 30,0T com uma frequência de 15H z . (Essa variação é produzida pela corrente em um fio enrolado em um ím
Um campo magnético uniforme B → é perpendicular ao plano de uma espira de raio r . O módulo do campo varia com o tempo de acrodo com a equação B = B o e t τ , onde B o e τ são constantes. Escreva uma
A figura 30-70a mostra uma espira retangular de resistência R = 0,020Ω , altura H = 1,5c m e comprimento D = 2,5c m , que é puxada com velocidade escalar constante v = 40c m / s e passa por duas regiõ