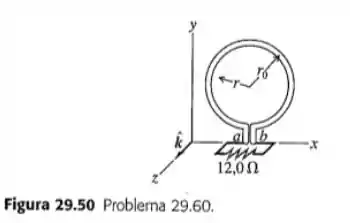
Um anel condutor circular, com raio , está sobre o plano em uma região onde existe um campo magnético uniforme , em que e permanece constante, é o tempo, é um vetor unitário orientado no sentido e e permanece constante. Nos pontos e (Figura 29.50), existe uma pequena abertura do anel, cujas extremidades são conectadas a fios que conduzem a corrente para um circuito externo com resistência . Não há nenhum campo magnético no local onde está o circuito externo.
Deduza uma relação, em função do tempo, para o fluxo magnético total através do anel.
Calcule a fem induzida no anel para . Qual a polaridade da fem?
Como o anel possui uma resistência interna, a corrente que flui através de no instante calculado no item é apenas . Determine a resistência do anel.
Calcule a fem induzida no anel para . Qual a polaridade da fem?
Determine o instante em que a corrente que flui através de inverte seu sentido.
Passo 1
Para resolver o nosso problema vamos aplicar a lei de Faraday para calcular a magnitude e a direção da fem induzida. Assim, tomemos que está saindo da página na figura isso significa que a fem em sentido anti-horário é positiva. Sendo assim, teremos
Passo 2
Continuando com a resolução do problema devemos lembrar que
Utilizando vamos ter
Nesse caso, temos positive, logo, está no sentido anti-horário. Agora, que temos o valor de e nos foi fornecido o valor da corrente induzida podemos calcular para o item fazendo
Mas devemos reparar que , então, temos
Passo 3
Para calcularmos a fem em vamos proceder de forma igual ao que calculamos no passo 2. Assim, temos
Por fim, para concluirmos o exercício percebamos que quando , então,
Pronto, finalmente resolvemos o exercício por completo.
Resposta