Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 31.1 - Ex. 22
Se o ingulo de incidencia for pequeno o suficiente,a aproximacao para angulos pequenos sen 0=0 pode ser usada para simplificar a lei da refracao de Snell.Determine o maximo valor do angulo para o qual a diferenca nao seja maior que 1 por cento do valor do seno do angulo.(Esta aproximacao sera usada em conexão com a formacio de imagens por superficies esfericas no Capitulo 32.)
Passo 1
Podemos expressar o erro relativo usando o pequeno ângulo de aproximação e então usando
1) métodos de tentativa e erro
2) um programa de planilha , ou
3) uma calculadora científica para resolver a equação transcendental que resulta da definição da função de erro igual a 0.01.
Expresse o erro relativo ao usar a aproximação de pequeno ângulo:
Passo 2
Um programa de planilha foi usado para traçar o seguinte gráfico de :
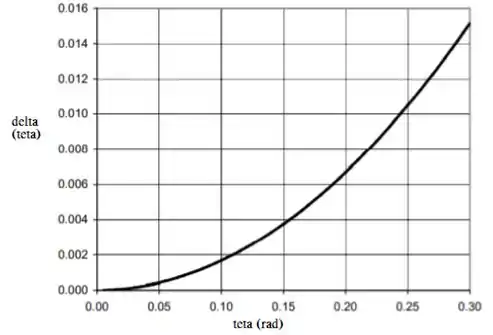
No gráfico, podemos ver que para radianos. Em graus, temos
Observações: Usando uma calculadora científica obtivemos radianos.
Resposta
Ver resolução