Enunciado
Física - Halliday - Vol 3- Ed: 4º - Capítulo 27.Exercícios e Problemas - Ex. 61
Uma lâmina de cobre de espessura b é introduzida exatamente no meio e entre as placas de um capacitor de placas paralelas, como é mostrado na Fig, 27-33. (a) Qual é a capacitância depois da introdução da placa? (b) Mantendo-se a carga q sobre as placas, qual é a razão entre as energias armazenadas antes e depois da introdução da lâmina? (c) Que trabalho é realizado sobre a lâmina durante a sua introdução? A lâmina é puxada ou temos de empurrá-la para o interior do capacitor?
Passo 1
Fala galera, bora lá!
Considere o seguinte esquema abaixo.
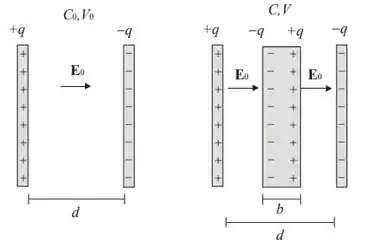
A introdução de um material condutor entre as placas de um capacitor carregado causa separação de cargas no condutor. Como o campo elétrico no interior do condutor deve ser zero (equilíbrio eletrostático), deduz-se que a separação de cargas no condutor gerou um campo elétrico que neutralizou o campo produzido pelas cargas nas placas.
Para que isso seja possível, as cargas induzidas no condutor devem ser iguais, em módulo, às cargas nas placas. O efeito líquido da introdução do material condutor é a criação de dois capacitores em série, de carga , área , separação das placas e capacitância . Chamando-se a capacitância da associação em série, ou seja, do capacitor original mais a placa de cobre introduzida, teremos:
Como
A capacitância depois da introdução da placa é
Passo 2
A razão entre a energia armazenada antes () e depois () da introdução da placa, vale:
Sabendo que . Temos,
A introdução da lâmina faz com que a energia potencial do sistema diminua.
Passo 3
Por definição, o trabalho realizado pela força elétrica vale:
Substituindo
Logo,
Quando a lâmina de cobre começa a ser introduzida no espaço entre as placas do capacitor, as cargas já existentes na s placas polarizam a extremidade da lâmina e as cargas induzidas são atraídas para dentro do capacitor. Como as cargas induzidas estão presas na lâmina, esta também é atraída para dentro do capacitor. Logo, a força externa precisa puxar a lâmina para fora das placas para neutralizar a força de atração e manter constante a velocidade de entrada da placa de cobre. A atração da lâmina pelas placas e sua aproximação, fazem com que a energia potencial do sistema diminua como revelou o resultado do item (b).