Uma lente delgada simétrica biconvexa é feita de vidro com índice de refração de e possui distância focal no ar igual a . A lente fecha uma abertura na extremidade esquerda de um tanque cheio de água. Na extremidade direita do tanque, oposta à lente, existe um espelho plano situado a uma distância de da lente. O índice de refração da água é igual a . (a) Determine a posição da imagem formada pelo sistema lente-água-espelho referente a um pequeno objeto fora do tanque situado sobre o eixo da lente a uma distância de à esquerda da lente. (b) A imagem é real ou virtual? (c) A imagem é direita ou invertida? (d) Se o objeto possui uma altura de , qual é a altura da imagem?

Beleza. A primeira coisa que a luz faz depois de sair do objeto é ser refratada na interface entre o ar e o vidro da lente.

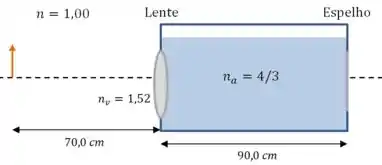
Substituindo com os valores que estão no desenho, e o raio que calculamos ali em cima:

Essa imagem vai servir de objeto para a segunda refração, em que a luz passa de dentro da lente para a água.

O sinal negativo diz que a primeira imagem se formou à esquerda da lente. Quando essa imagem serve de objeto para a lente, temos:

Então:

O sinal do raio de curvatura muda porque agora estamos do outro lado do centro de curvatura da lente (indo de dentro pra fora).

Isso quer dizer que a imagem está à direita da lente, e a do espelho plano.

Logo em seguida, o espelho plano vai gerar uma imagem à sua esquerda, e então a distância até a lente vai ser:

À esquerda da lente! O sinal negativo aparece porque essa imagem serve de objeto virtual para a lente.

Agora vamos fazer o mesmo caminho de antes, mas ao contrário.

Primeiro a imagem é refratada na interface entre a água e a lente:

E seguindo a mesma lógica de antes, agora passamos da lente para o ar:

Ou seja, a imagem final é formada à esquerda da lente. (Já que temos uma lente e um espelho, só faz sentido que a imagem esteja à esquerda mesmo!)

Ok, agora pra determinar as outras propriedades da imagem, vamos calcular a ampliação total.

A ampliação só é diferente de quando estamos passando pela lente, o que aconteceu quatro vezes, então:

E a fórmula para cada uma dessas ampliações é:

Então temos que voltar nos passos de cima para ver quais eram esses valores em cada passo:

E essa confusão toda vai dar no seguinte:

Agora vamos às perguntas.

(b) Como na última etapa a gente acabou com , a imagem é real.

(c) Como a ampliação resultante é , a imagem é invertida.

(d) Já que a altura original do objeto era e a ampliação é , a altura final é:

Ou seja, a altura final é . O sinal só indica que a imagem é invertida.